Visualizzare la vera estensione della Maledizione della Dimensionalità

Visualizzare la vera estensione della Maledizione della Dimensionalità.

Utilizzo del metodo Monte Carlo per visualizzare il comportamento delle osservazioni con un gran numero di caratteristiche

Immagina un dataset, composto da un certo numero di osservazioni, ognuna delle quali ha N caratteristiche. Se converti tutte le caratteristiche in una rappresentazione numerica, potresti dire che ogni osservazione è un punto in uno spazio N-dimensionale.

Quando N è basso, le relazioni tra i punti sono esattamente quelle che ti aspetteresti intuitivamente. Ma a volte N diventa molto grande – questo potrebbe accadere, ad esempio, se stai creando molte caratteristiche tramite codifica one-hot, ecc. Per valori molto grandi di N, le osservazioni si comportano come se fossero sparse, o come se le distanze tra loro fossero in qualche modo più grandi di quanto ci si aspetterebbe.

Il fenomeno è reale. Man mano che il numero di dimensioni N cresce, e tutto il resto rimane lo stesso, il volume N che contiene le tue osservazioni aumenta effettivamente in un certo senso (o almeno il numero di gradi di libertà diventa più grande), e le distanze euclidee tra le osservazioni aumentano anche. Il gruppo di punti diventa effettivamente più sparso. Questa è la base geometrica per la maledizione della dimensionalità . Il comportamento dei modelli e delle tecniche applicate al dataset sarà influenzato come conseguenza di questi cambiamenti.

Molte cose possono andare storte se il numero di caratteristiche è molto grande. Avere più caratteristiche rispetto alle osservazioni è una configurazione tipica per i modelli che fanno overfitting durante l’addestramento. Qualsiasi ricerca esaustiva in uno spazio del genere (ad esempio, GridSearch) diventa meno efficiente: hai bisogno di più prove per coprire gli stessi intervalli lungo qualsiasi asse. Un effetto sottile ha un impatto su qualsiasi modello basato sulla distanza o sulla vicinanza: man mano che il numero di dimensioni cresce a valori molto grandi, se consideri un punto delle tue osservazioni, tutti gli altri punti sembrano essere lontani e in qualche modo quasi equidistanti – poiché questi modelli si basano sulla distanza per fare il loro lavoro, l’omogeneizzazione delle differenze di distanza rende il loro lavoro molto più difficile. Ad esempio, il clustering non funziona così bene se tutti i punti sembrano essere quasi equidistanti.

• Gamificare l’etichettatura dei dati medici per far avanzare l’IA
• Un modo molto sottovalutato per costruire capitale di carriera in Data Science
• I Top 3 trend dell’architettura dei dati (e come gli LLM influenzeranno loro)

Per tutte queste ragioni, e altre ancora, sono state create tecniche come PCA, LDA, ecc. – nel tentativo di allontanarsi dalla geometria peculiare degli spazi con un gran numero di dimensioni e di sintetizzare il dataset in un numero di dimensioni più compatibile con le informazioni effettive contenute al suo interno.

È difficile percepire intuitivamente la vera entità di questo fenomeno, e gli spazi con più di 3 dimensioni sono estremamente difficili da visualizzare, quindi facciamo alcune semplici visualizzazioni 2D per aiutare la nostra intuizione. C’è una base geometrica per il motivo per cui la dimensionalità può diventare un problema, ed è quello che visualizzeremo qui. Se non hai mai visto questo prima, i risultati potrebbero essere sorprendenti: la geometria degli spazi ad alta dimensionalità è molto più complessa di quanto l’intuizione tipica suggerisca.

Volume

Considera un quadrato di dimensione 1, centrato nell’origine. Nel quadrato, si inscrive un cerchio.

Questo è il setup in 2 dimensioni. Ora pensa al caso generale, N-dimensionale. In 3 dimensioni, hai una sfera inscritta in un cubo. Oltre a ciò, hai una N-sfera inscritta in un N-cubo, che è il modo più generale di metterlo. Per semplicità, ci riferiremo a questi oggetti come “sfera” e “cubo”, indipendentemente dal numero di dimensioni che hanno.

Il volume del cubo è fisso, è sempre 1. La domanda è: cosa succede al volume della sfera al variare del numero di dimensioni N?

Risponderemo alla domanda in modo sperimentale, utilizzando il metodo Monte Carlo. Genereremo un gran numero di punti, distribuiti in modo uniforme ma casualmente all’interno del cubo. Per ogni punto calcoliamo la sua distanza dall’origine: se quella distanza è inferiore a 0,5 (il raggio della sfera), allora il punto è all’interno della sfera.

Se dividiamo il numero di punti all’interno della sfera per il numero totale di punti, otterremo un’approssimazione del rapporto tra il volume della sfera e il volume del cubo. Poiché il volume del cubo è 1, il rapporto sarà uguale al volume della sfera. L’approssimazione migliora quando il numero totale di punti è grande.

In altre parole, il rapporto inside_points / total_points approssimerà il volume della sfera.

Il codice è piuttosto semplice. Dato che abbiamo bisogno di molti punti, è necessario evitare i loop espliciti. Potremmo usare NumPy, ma è solo per CPU e single-threaded, quindi sarebbe lento. Possibili alternative: CuPy (GPU), Jax (CPU o GPU), PyTorch (CPU o GPU), ecc. Useremo PyTorch, ma il codice NumPy sarebbe quasi identico.

Se segui le istruzioni annidate di torch, generiamo 100 milioni di punti casuali, calcoliamo le loro distanze dall’origine, contiamo i punti all’interno della sfera e dividiamo il conteggio per il numero totale di punti. L’array ratio conterrà il volume della sfera in diverse dimensioni.

I parametri regolabili sono impostati per una GPU con 24 GB di memoria, quindi adattali se hai hardware diverso.

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")# forza CP# device = 'cpu'# riduci d_max se ci sono troppi valori di ratio pari a 0.0d_max = 22# riduci n se esaurisci la memoria n = 10**8ratio = np.zeros(d_max)for d in tqdm(range(d_max, 0, -1)):    torch.manual_seed(0)    # combina grandi istruzioni di tensori per una migliore allocazione della memoria    ratio[d - 1] = (        torch.sum(            torch.sqrt(                torch.sum(torch.pow(torch.rand((n, d), device=device) - 0.5, 2), dim=1)            )            <= 0.5        ).item()        / n    )# pulisci la memoriatorch.cuda.empty_cache()

Visualizziamo i risultati:

N=1 è banale: sia la “sfera” che il “cubo” sono solo segmenti lineari e sono uguali, quindi il “volume” della “sfera” è 1. Per N=2 e N=3, dovresti ricordare i risultati della geometria delle scuole superiori e notare che questa simulazione è molto vicina ai valori esatti.

Ma all’aumentare di N, succede qualcosa di molto drammatico: il volume della sfera crolla come una pietra. È già vicino a 0 quando N=10 e scende al di sotto della precisione in virgola mobile di questa simulazione poco dopo N=20 circa. Oltre quel punto, il codice calcola il volume della sfera come 0.0 (è solo un’approssimazione).

>>> print(list(ratio))[1.0, 0.78548005, 0.52364381, 0.30841056, 0.16450286, 0.08075666, 0.03688062, 0.015852, 0.00645304, 0.00249584, 0.00092725, 0.00032921, 0.00011305, 3.766e-05, 1.14e-05, 3.29e-06, 9.9e-07, 2.8e-07, 8e-08, 3e-08, 2e-08, 0.0]

Per valori elevati di N, quasi tutto il volume del cubo si trova negli angoli. La regione centrale, che contiene la sfera, diventa insignificante in confronto. Negli spazi di dimensioni elevate, gli angoli diventano molto importanti. La maggior parte del volume “migra” negli angoli. Questo avviene estremamente velocemente all’aumentare di N.

Un altro modo di vederlo: la sfera è la “vicinanza” dell’origine. All’aumentare di N, i punti semplicemente scompaiono da quella vicinanza. L’origine non è davvero così speciale, quindi ciò che accade alla sua vicinanza deve accadere a tutte le vicinanze ovunque. La stessa nozione di “vicinanza” subisce un grande cambiamento. I quartieri si svuotano insieme all’aumento di N.

Ho eseguito questa simulazione per la prima volta anni fa e ricordo vividamente quanto fosse sorprendente questo risultato, quanto velocemente il volume della sfera si schianta a 0 all’aumentare di N. Dopo aver controllato il codice e non aver trovato errori, la mia reazione è stata: salva il lavoro, blocca lo schermo, esci, fai una passeggiata e rifletti su ciò che hai appena visto. 🙂

Distanza lineare

Calcoliamo la diagonale del cubo come funzione di N. Questo è banale, poiché la diagonale è letteralmente sqrt(N), quindi il codice è troppo semplice per essere incluso qui. E questi sono i risultati:

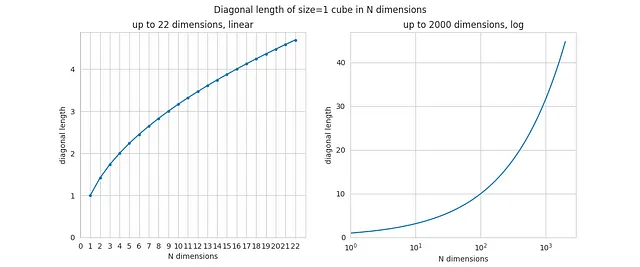
Anche per N=2 e N=3 dovresti riconoscere i risultati dalla geometria (la diagonale del quadrato e del normale cubo a 3 dimensioni). Ma all’aumentare di N, la diagonale aumenta anche, e la sua crescita è illimitata.

Questo può sembrare molto controintuitivo, ma anche se la dimensione del lato del cubo rimane costante (e uguale a 1), la sua diagonale può crescere arbitrariamente grande, aumentando N. Già per N=1000, la lunghezza della diagonale è di circa 32. In teoria, se il lato del cubo è di 1 metro, ci sarà uno spazio con molte dimensioni in cui la diagonale del cubo sarà di 1 chilometro!

Anche se la distanza lungo il lato rimane la stessa, la diagonale continua a crescere con il numero di dimensioni.

Ogni volta che viene aggiunta una nuova dimensione allo spazio, spuntano nuovi lati, facce, ecc., la configurazione della regione dell’angolo diventa più complessa, con più gradi di libertà, e la diagonale misurerà un po’ di più.

Distanze tra osservazioni

Come per le distanze tra osservazioni o punti? Supponiamo che generiamo un numero fisso di punti casuali, e poi calcoliamo la distanza media tra due punti e la distanza media al punto più vicino di ogni punto. Tutti i punti sono sempre contenuti nel cubo. Cosa succede alle distanze medie all’aumentare di N? Eseguiamo un’altra simulazione.

Si prega di notare l’approccio conservativo alla gestione della memoria. Questo è importante, poiché le strutture dati utilizzate qui sono piuttosto grandi.

n_points_d = 10**3# quante coppie di punti ci sonodist_count = n_points_d * (n_points_d - 1) / 2# usiamo la matrice completa delle distanze tra coppie,# quindi ogni distanza verrà contata due voltadist_count = 2 * dist_countd_max = d_max_diagavg_dist = np.zeros(d_max)avg_dist_nn = np.zeros(d_max)for d in tqdm(range(d_max, 0, -1)):    torch.manual_seed(0)    # generiamo punti casuali    point_coordinates = torch.rand((n_points_d, d), device=device)    # calcoliamo le differenze delle coordinate dei punti su tutti gli assi    coord_diffs = point_coordinates.unsqueeze(1) - point_coordinates    del point_coordinates    # eleviamo al quadrato le differenze delle coordinate    diffs_squared = torch.pow(coord_diffs, 2)    del coord_diffs    # calcoliamo le distanze tra tutti i 2 punti    distances_full = torch.sqrt(torch.sum(diffs_squared, dim=2))    del diffs_squared    # calcoliamo la distanza media tra i punti    avg_dist[d - 1] = torch.sum(distances_full).item() / dist_count    # calcoliamo le distanze ai vicini più vicini    distances_full[distances_full == 0.0] = np.sqrt(d) + 1    distances_nn, _ = torch.min(distances_full, dim=0)    del distances_full    # calcoliamo la distanza media ai vicini più vicini    avg_dist_nn[d - 1] = torch.mean(distances_nn).item()    del distances_nntorch.cuda.empty_cache()

Usiamo molti meno punti qui (solo 1000) perché la dimensione delle principali strutture dati aumenta con N^2, quindi finiremmo rapidamente senza memoria se generassimo troppi punti. Tuttavia, i risultati approssimati dovrebbero essere abbastanza vicini ai valori effettivi.

Questo è la distanza media tra due punti, su 1000, come funzione di N:

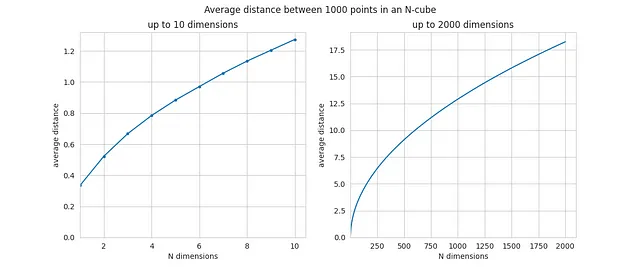
Per valori piccoli di N, la distanza media è qualcosa come 0.5 o 1. Ma all’aumentare di N, la distanza media inizia a crescere, ed è già vicina a 18 quando N=2000. L’aumento è sostanziale.

Questa è la distanza media al vicino più vicino, in funzione di N:

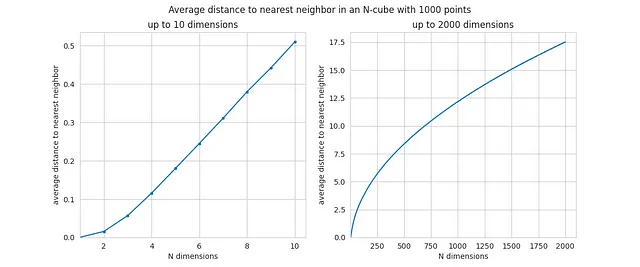
L’aumento qui è ancora più drammatico, poiché i valori sono molto piccoli quando N è inferiore a 10 e i punti sono vicini in uno spazio di bassa dimensionalità. Per grandi valori di N, la distanza media al vicino più vicino si avvicina effettivamente alla distanza media tra due punti – in altre parole, il vuoto delle immediate vicinanze domina le misurazioni.

Ecco perché abbiamo detto all’inizio che i punti diventano quasi equidistanti in spazi ad alta dimensionalità – le distanze medie e le distanze più brevi diventano quasi le stesse. Qui hai la prova dalla simulazione e un’intuizione sulla forza del fenomeno.

All’aumentare del numero di dimensioni N, tutti i punti si allontanano l’uno dall’altro, anche se le loro coordinate sono confinate nello stesso intervallo ristretto (-0,5, +0,5). Il gruppo di punti diventa effettivamente sempre più sparso semplicemente creando più dimensioni. L’aumento copre un paio di ordini di grandezza quando le dimensioni passano da poche unità a qualche migliaio. È un aumento molto grande.

Conclusioni

La maledizione della dimensionalità è un fenomeno reale. A parità di condizioni, all’aumentare del numero di dimensioni (o caratteristiche), i punti (o osservazioni) si allontanano rapidamente l’uno dall’altro. Effettivamente c’è più spazio lì dentro, anche se gli intervalli lineari lungo gli assi sono gli stessi. Tutte le vicinanze si svuotano e ogni punto finisce per stare da solo in uno spazio ad alta dimensionalità.

Questo dovrebbe fornire un’idea del fatto che alcune tecniche (clustering, vari modelli, ecc.) possono comportarsi in modo diverso quando il numero delle caratteristiche cambia sostanzialmente. Poche osservazioni, combinate con un gran numero di caratteristiche, possono portare a risultati sub-ottimali – e sebbene la maledizione della dimensionalità non sia l’unico motivo per questo, può essere uno dei motivi.

In generale, il numero di osservazioni dovrebbe “mantenere il passo” con il numero di caratteristiche – le regole esatte dipendono da molti fattori.

Se non altro, questo articolo dovrebbe fornire una panoramica intuitiva delle proprietà degli spazi ad alta dimensionalità, che sono difficili da visualizzare. Alcune delle tendenze sono sorprendentemente forti, e ora dovresti avere un’idea di quanto siano forti.

Tutto il codice utilizzato in questo articolo è qui:

misc/curse_dimensionality_article/n_sphere.ipynb at master · FlorinAndrei/misc

roba casuale. Contribuisci allo sviluppo di FlorinAndrei/misc creando un account su GitHub.

github.com

Tutte le immagini utilizzate in questo articolo sono create dall’autore (vedi il link al codice sopra).