Trasformata di Fourier per le serie temporali Spiegazione della convoluzione rapida con numpy

Spiegazione della Trasformata di Fourier per le serie temporali e la convoluzione rapida con numpy.

Implementazione da zero vs numpy

L’algoritmo della trasformata di Fourier è considerato una delle più grandi scoperte di tutta la matematica. Il matematico francese Jean-Baptiste Joseph Fourier ha gettato le basi per l’analisi armonica nel suo libro “Théorie analytique de la chaleur” nel 1822. Oggi, la trasformata di Fourier e tutte le sue varianti costituiscono la base del nostro mondo moderno, alimentando tecnologie come la compressione, la comunicazione, l’elaborazione delle immagini.

Questo meraviglioso framework fornisce anche ottimi strumenti per l’analisi delle serie temporali… ed è per questo che siamo qui!

Questo post fa parte di una serie sulla trasformata di Fourier. Oggi parleremo di convoluzione e di come la trasformata di Fourier fornisce il modo più veloce per farlo.

Tutte le figure ed equazioni sono state realizzate dall’autore.

• EDA con Polars Guida passo passo per gli utenti di Pandas (Parte 1)
• Sbloccare il successo della modellazione dei dati 3 tabelle contestuali indispensabili
• Come diventare virale usando ChatGPT

Definizione della Trasformata di Fourier Discreta (DFT)

Iniziamo con le definizioni di base. La trasformata di Fourier discreta per una sequenza di tempo discreta x di N elementi è la seguente:

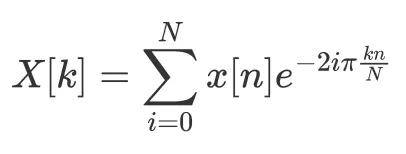
dove k indica la k-esima frequenza dello spettro di x. Nota che alcuni autori aggiungono un fattore di scala di 1/N a questa definizione, ma non è di grande importanza per questo post – tutto sommato è solo una questione di definizione e di attenersi ad essa.

La trasformata di Fourier inversa è quindi (dato che abbiamo definito la trasformata di Fourier diretta):

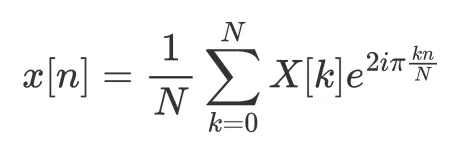
Detto ciò, uno dei teoremi più importanti sulla trasformata di Fourier è che la convoluzione in uno spazio è equivalente alla moltiplicazione nell’altro. In altre parole, la trasformata di Fourier di un prodotto è la convoluzione dei rispettivi spettri di Fourier, e la trasformata di Fourier di una convoluzione è il prodotto dei rispettivi spettri di Fourier.

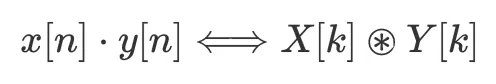
e

dove il punto rappresenta il prodotto standard (moltiplicazione) e l’asterisco cerchiato rappresenta la convoluzione circolare.

Due note importanti:

• Segnale periodico: Il framework dell’analisi di Fourier considera che i segnali che gestiamo siano periodici. In altre parole, si ripetono da meno infinito a più infinito. Tuttavia, non è sempre pratico gestire tali segnali con un computer a memoria finita, quindi giochiamo solo con un periodo, come vedremo in seguito.
• Convoluzione circolare: Il teorema della convoluzione stabilisce che la moltiplicazione è equivalente alla convoluzione circolare, che è leggermente diversa dalla convoluzione lineare, a cui siamo più abituati. Come vedremo, non è così diversa e nemmeno così complicata.

Convoluzione circolare vs convoluzione lineare

Se sei familiare con la convoluzione lineare, spesso semplicemente chiamata ‘convoluzione’, non sarai confuso dalla convoluzione circolare. Fondamentalmente, la convoluzione circolare è solo il modo per convolvere segnali periodici. Come puoi immaginare, la convoluzione lineare ha senso solo per segnali di lunghezza finita, che non si estendono da meno infinito a più infinito. Nel nostro caso, nel contesto dell’analisi di Fourier, i nostri segnali sono periodici e quindi non soddisfano questa condizione. Non possiamo parlare di (convoluzione) lineare.

Tuttavia, possiamo ancora intuire un’operazione simile alla convoluzione lineare sui nostri segnali periodici: basta convolvere il segnale periodico su una lunghezza di un periodo. Questo è ciò che fa la convoluzione circolare: convolve due segnali periodici della stessa lunghezza lungo un periodo.

Per convincerti ulteriormente della differenza, confronta entrambe le formule per la convoluzione lineare discreta e la convoluzione circolare discreta:

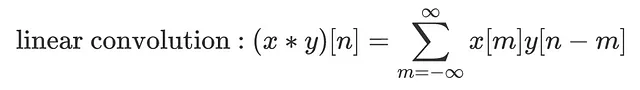
Nota le differenze:

– limiti: la convoluzione lineare utilizza campioni da meno infinito a più infinito — come già detto, in questo contesto x e y hanno energia finita, quindi la somma ha senso. Per la convoluzione circolare, abbiamo solo bisogno di ciò che è accaduto in un intervallo di periodo, quindi la somma si estende solo su un periodo.

– indici circolari: nella convoluzione circolare, “avvolgiamo” l’indice di y usando un’operazione modulo con una lunghezza di N. Questo è solo un modo per garantire che y sia considerato periodico con un periodo di N: quando vogliamo conoscere il valore di y nella posizione k, usiamo semplicemente il valore di y nella posizione k%N – dato che y è periodico di N, otteniamo il valore corretto. Ancora una volta, questo è solo un modo matematico per gestire sequenze di campioni periodiche di lunghezza infinita.

Implementazione in numpy

Numpy fornisce ottimi strumenti per segnali di lunghezza finita: e questa è una buona notizia perché, come abbiamo appena visto, il nostro segnale periodico di lunghezza infinita può essere rappresentato con un solo periodo.

Creiamo una semplice classe per rappresentare tali segnali. Aggiungiamo un metodo per tracciare rapidamente l’array, così come un periodo aggiuntivo prima e dopo l’array “base”, per tenere presente che stiamo trattando una sequenza periodica.

Guardiamo due esempi: prima con una sequenza sinusoidale campionata, poi con una sequenza lineare. Entrambi sono considerati N-periodici (N=10 in questo caso).

Convoluzione circolare, il modo lento

Implementiamo ora l’equazione di convoluzione circolare vista in precedenza. Utilizzando l’indicizzazione e l’operatore modulo, è abbastanza semplice:

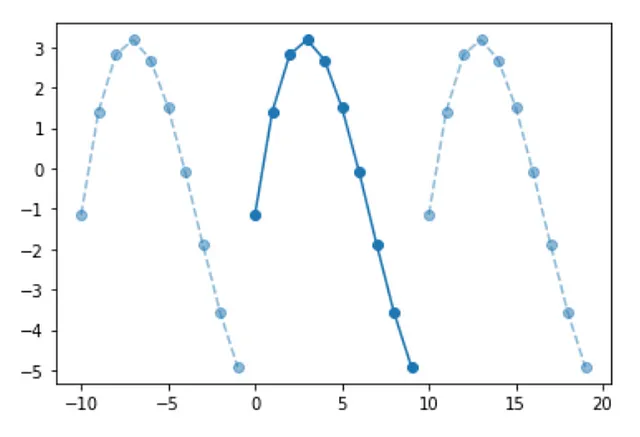
È fantastico, ora possiamo vedere come appare la convoluzione circolare tra due segnali. Mettendo tutto in un’unica figura:

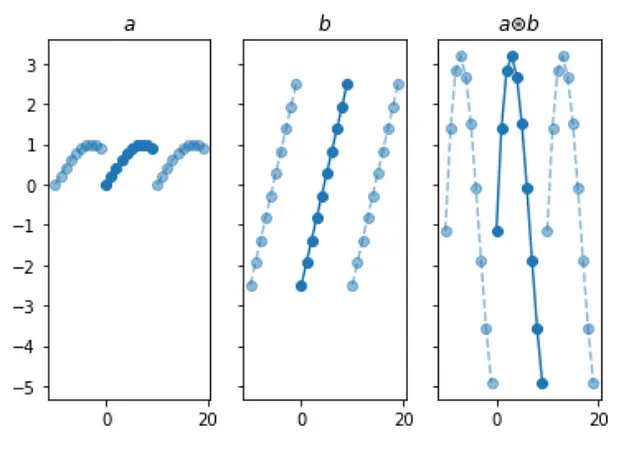
Ora questa soluzione funziona molto bene, ma ha un grave difetto: è lenta. Come puoi vedere, dobbiamo passare attraverso 2 cicli nidificati per calcolare il risultato: uno per ogni posizione nell’array risultante e uno per calcolare il risultato in quella posizione: diciamo che l’algoritmo è O(N²), all’aumentare di N il numero di operazioni aumenterà al quadrato di N.

Per array piccoli come quelli nell’esempio, non è un problema, ma quando il tuo array crescerà diventerà un problema molto serio.

Inoltre, i cicli sui dati numerici sono considerati per lo più una pratica scorretta in python. Deve esserci un modo migliore…

Convoluzione circolare, il modo di Fourier

E qui entrano in gioco la trasformata di Fourier e il teorema della convoluzione. A causa del modo in cui è implementata la trasformata di Fourier discreta, in modo molto rapido e ottimizzato utilizzando la Trasformata di Fourier Veloce (FFT), l’operazione è **molto** rapida (diciamo che la FFT è O(N log N), che è molto migliore di O(N²)).

Utilizzando il teorema della convoluzione, possiamo utilizzare il fatto che il prodotto della TFD di due sequenze, quando viene trasformato nuovamente nel dominio temporale utilizzando la TFD inversa, otteniamo la convoluzione delle sequenze temporali di input. In altre parole, abbiamo:

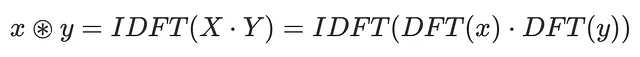
dove TFD rappresenta la Trasformata di Fourier discreta e TFD inversa l’operazione inversa.

Possiamo quindi implementare facilmente questo algoritmo per calcolare la convoluzione di x e y utilizzando numpy:

Confronto numerico e temporale

Per concludere, verifichiamo che entrambi gli approcci producano gli stessi risultati e confrontiamo il tempo impiegato da Python per calcolare la convoluzione circolare utilizzando entrambe le tecniche:

È una corrispondenza perfetta! Entrambi sono rigorosamente equivalenti in termini di valori numerici.

Ora per il confronto temporale:

E i risultati sono:

• per N=10 campioni, la TFD è più veloce di un fattore di 6
• per N=1000 campioni, la TFD è più veloce di un fattore di circa 10000

È enorme! Considera ora cosa può offrirti quando analizzi serie temporali con migliaia e migliaia di campioni!

Conclusione

In questo post abbiamo visto che la trasformata di Fourier è uno strumento potente, specialmente grazie al teorema della convoluzione che ci consente di calcolare la convoluzione in modo molto efficiente. Abbiamo visto che le convoluzioni lineari e circolari non sono esattamente la stessa operazione, ma si basano entrambe su una convoluzione.

Iscriviti per ricevere direttamente sul tuo feed i futuri articoli sulla trasformata di Fourier!

Inoltre, dai un’occhiata ai miei altri articoli e se ti piace qualcuno di essi, per favore iscriviti: mi aiuterà molto a raggiungere il mio obiettivo di 100 iscritti:

Risoluzione 300 volte più veloce del metodo delle differenze finite utilizzando NumPy | di Yoann Mocquin | Towards Data Science (VoAGI.com)

PCA/LDA/ICA: un confronto degli algoritmi di analisi dei componenti | di Yoann Mocquin | Towards Data Science (VoAGI.com)

Avvolgimento dell’array di NumPy. L’approccio del contenitore. | di Yoann Mocquin | Towards Data Science (VoAGI.com)

Approfondimento su Seaborn: palette di colori | di Yoann Mocquin | Analytics Vidhya | VoAGI