Optimizzazione del controllore PID Un approccio di discesa del gradiente

Optimizzazione del controllore PID con discesa del gradiente

Utilizzo del machine learning per risolvere problemi di ottimizzazione ingegneristica

Machine learning. Deep learning. Intelligenza artificiale. Sempre più persone utilizzano queste tecnologie ogni giorno. Ciò è stato in gran parte determinato dall’avvento dei Large Language Models utilizzati da ChatGPT, Bard e altri. Nonostante il loro uso diffuso, relativamente poche persone sono familiari con i metodi sottostanti a queste tecnologie.

In questo articolo, esamineremo uno dei metodi fondamentali utilizzati nel machine learning: l’algoritmo del gradiente discendente.

Invece di analizzare il gradiente discendente attraverso il prisma delle reti neurali, dove viene utilizzato per ottimizzare i pesi e i bias della rete, esamineremo l’algoritmo come uno strumento per risolvere problemi classici di ottimizzazione ingegneristica.

In particolare, utilizzeremo il gradiente discendente per regolare i guadagni di un controllore PID (Proporzionale-Integrale-Derivativo) per un sistema di controllo della velocità di crociera dell’auto.

• Input vocale e linguaggio naturale per la tua app mobile utilizzando LLM
• Introduzione alle rappresentazioni di frasi dell’IA
• Perfeziona il tuo LLM senza sfruttare al massimo la tua GPU

Le motivazioni per seguire questo approccio sono due:

Innanzitutto, l’ottimizzazione dei pesi e dei bias in una rete neurale è un problema ad alta dimensionalità. Ci sono molte parti in movimento e penso che queste distraggano dall’utilità sottostante del gradiente discendente per la soluzione di problemi di ottimizzazione.

In secondo luogo, come vedrete, il gradiente discendente può essere uno strumento potente quando applicato a problemi di ingegneria classici come la taratura del controllore PID, la cinematica inversa nella robotica e l’ottimizzazione della topologia. Il gradiente discendente è uno strumento che, a mio parere, più ingegneri dovrebbero conoscere e saper utilizzare.

Dopo aver letto questo articolo, comprenderete cosa è un controllore PID, come funziona l’algoritmo del gradiente discendente e come può essere applicato per risolvere problemi classici di ottimizzazione ingegneristica. Potreste essere motivati a utilizzare il gradiente discendente per affrontare sfide di ottimizzazione personali.

Tutto il codice utilizzato in questo articolo è disponibile qui su GitHub.

Cos’è un controllore PID?

Un controllore PID è un meccanismo di controllo a feedback ampiamente utilizzato nell’ingegneria e nei sistemi automatizzati. Si propone di mantenere un valore di riferimento desiderato mediante l’aggiustamento continuo del segnale di controllo in base all’errore tra il valore di riferimento e l’output misurato del sistema (la variabile di processo).

I controllori PID trovano ampie applicazioni in vari settori e ambiti. Sono ampiamente utilizzati nei sistemi di controllo di processo, come il controllo della temperatura nella produzione, il controllo del flusso nelle impianti chimici e il controllo della pressione nei sistemi di climatizzazione. I controllori PID vengono anche impiegati nella robotica per il posizionamento preciso e il controllo del movimento, così come nei sistemi automobilistici per il controllo dell’acceleratore, la regolazione della velocità del motore e i sistemi antibloccaggio dei freni. Giocano un ruolo vitale nelle applicazioni aerospaziali e dell’aviazione, compresi gli autopiloti degli aeromobili e i sistemi di controllo dell’assetto.

Un controllore PID è composto da tre componenti: il termine proporzionale, il termine integrale e il termine derivativo. Il termine proporzionale fornisce una risposta immediata all’errore corrente, il termine integrale accumula e corregge gli errori passati, e il termine derivativo predice e contrasta le tendenze future dell’errore.

Il loop di controllo di un controllore PID è presentato nel diagramma a blocchi sopra. r(t) è il valore di riferimento e y(t) è la variabile di processo. La variabile di processo viene sottratta dal valore di riferimento per ottenere il segnale di errore, e(t).

Il segnale di controllo, u(t), è la somma dei termini proporzionale, integrale e derivativo. Il segnale di controllo è l’input del processo e questo, a sua volta, provoca l’aggiornamento della variabile di processo.

Segnale di controllo del controllore PID u(t)

L’algoritmo del gradiente discendente

Il gradiente discendente è un algoritmo di ottimizzazione comunemente utilizzato nel machine learning e nell’ottimizzazione matematica. Si propone di trovare il minimo di una data funzione di costo mediante l’aggiustamento iterativo dei parametri in base al gradiente della funzione di costo. Il gradiente indica la direzione della pendenza più ripida, quindi prendendo passi nella direzione opposta, l’algoritmo converge gradualmente verso la soluzione ottimale.

Un singolo passo di aggiornamento di discesa del gradiente è definito come:

Passo di aggiornamento di discesa del gradiente

Dove aₙ è un vettore di parametri di input. L’apice n denota l’iterazione. f(aₙ) è una funzione di costo multivariabile e ∇f(a) è il gradiente di quella funzione di costo. ∇f(aₙ) rappresenta la direzione di massima ascensione, quindi viene sottratto da aₙ per ridurre la funzione di costo nella successiva iterazione. 𝛾 è il tasso di apprendimento che determina la dimensione del passo ad ogni iterazione.

Deve essere selezionato un valore appropriato per 𝛾. Troppo grande e i passi compiuti ad ogni iterazione saranno troppo grandi e causeranno la non convergenza dell’algoritmo di discesa del gradiente. Troppo piccolo e l’algoritmo di discesa del gradiente sarà computazionalmente oneroso e richiederà molto tempo per convergere.

La discesa del gradiente viene applicata in una vasta gamma di campi e discipline. Nell’apprendimento automatico e nell’apprendimento profondo, è un algoritmo di ottimizzazione fondamentale utilizzato per addestrare reti neurali e ottimizzare i loro parametri. Aggiornando iterativamente i pesi e i bias della rete in base al gradiente della funzione di costo, la discesa del gradiente consente alla rete di imparare e migliorare le sue prestazioni nel tempo.

Oltre all’apprendimento automatico, la discesa del gradiente è utilizzata in vari problemi di ottimizzazione in ingegneria, fisica, economia e altri settori. Aiuta nella stima dei parametri, nell’identificazione dei sistemi, nell’elaborazione dei segnali, nella ricostruzione delle immagini e in molte altre attività che richiedono la ricerca del minimo o del massimo di una funzione. La versatilità ed efficacia della discesa del gradiente la rendono uno strumento essenziale per risolvere problemi di ottimizzazione e migliorare modelli e sistemi in campi diversi.

Ottimizzazione dei guadagni del controllore PID utilizzando la discesa del gradiente

Sono disponibili diversi metodi per sintonizzare un controllore PID. Questi includono il metodo di sintonizzazione manuale e metodi euristici come il metodo di Ziegler-Nichols. Il metodo di sintonizzazione manuale può richiedere tempo ed è possibile che sia necessaria più di una iterazione per trovare valori ottimali, mentre il metodo di Ziegler-Nichols spesso produce guadagni aggressivi e un’elevata sovrapposizione che significa che non è adatto a determinate applicazioni.

Qui viene presentato un approccio di discesa del gradiente all’ottimizzazione del controllore PID. Ottimizzeremo il sistema di controllo di un sistema di controllo della velocità di una macchina soggetto a una variazione a gradino nel punto di impostazione.

Controllando la posizione del pedale, l’obiettivo del controllore è accelerare la macchina fino alla velocità di riferimento con il minimo overshoot, tempo di assestamento e errore allo stato stazionario.

La macchina è soggetta a una forza di guida proporzionale alla posizione del pedale. Le forze di resistenza al rotolamento e di trascinamento aerodinamico agiscono nella direzione opposta alla forza di guida. La posizione del pedale è controllata dal controllore PID e limitata a un intervallo compreso tra -50% e 100%. Quando la posizione del pedale è negativa, la macchina sta frenando.

È utile avere un modello del sistema durante la sintonizzazione dei guadagni del controllore PID. In questo modo possiamo simulare la risposta del sistema. A tal fine, ho implementato una classe Car in Python:

import numpy as npclass Car:    def __init__(self, mass, Crr, Cd, A, Fp):        self.mass = mass # [kg]        self.Crr = Crr # [-]        self.Cd = Cd # [-]        self.A = A # [m^2]        self.Fp = Fp # [N/%]        def get_acceleration(self, pedal, velocity):        # Constants        rho = 1.225 # [kg/m^3]        g = 9.81 # [m/s^2]        # Driving force        driving_force = self.Fp * pedal        # Rolling resistance force        rolling_resistance_force = self.Crr * (self.mass * g)        # Drag force        drag_force = 0.5 * rho * (velocity ** 2) * self.Cd * self.A        acceleration = (driving_force - rolling_resistance_force - drag_force) / self.mass        return acceleration        def simulate(self, nsteps, dt, velocity, setpoint, pid_controller):        pedal_s = np.zeros(nsteps)        velocity_s = np.zeros(nsteps)        time = np.zeros(nsteps)        velocity_s[0] = velocity        for i in range(nsteps - 1):            # Get pedal position [%]            pedal = pid_controller.compute(setpoint, velocity, dt)            pedal = np.clip(pedal, -50, 100)            pedal_s[i] = pedal            # Get acceleration            acceleration = self.get_acceleration(pedal, velocity)                        # Get velocity            velocity = velocity_s[i] + acceleration * dt            velocity_s[i+1] = velocity            time[i+1] = time[i] + dt                return pedal_s, velocity_s, time

La classe PIDController è implementata come:

class PIDController:    def __init__(self, Kp, Ki, Kd):        self.Kp = Kp        self.Ki = Ki        self.Kd = Kd        self.error_sum = 0        self.last_error = 0        def compute(self, setpoint, process_variable, dt):        error = setpoint - process_variable                # Termine Proporzionale        P = self.Kp * error                # Termine Integrale        self.error_sum += error * dt        I = self.Ki * self.error_sum                # Termine Derivativo        D = self.Kd * (error - self.last_error)        self.last_error = error                # Uscita PID        output = P + I + D                return output

Adottare questo approccio di programmazione ad oggetti rende molto più facile impostare ed eseguire più simulazioni con diversi guadagni del controllore PID, come dobbiamo fare quando eseguiamo l’algoritmo della discesa del gradiente.

La classe GradientDescent è implementata come:

class GradientDescent:    def __init__(self, a, learning_rate, cost_function, a_min=None, a_max=None):        self.a = a        self.learning_rate = learning_rate        self.cost_function = cost_function        self.a_min = a_min        self.a_max = a_max        self.G = np.zeros([len(a), len(a)])        self.points = []        self.result = []        def grad(self, a):        h = 0.0000001        a_h = a + (np.eye(len(a)) * h)        cost_function_at_a = self.cost_function(a)        grad = []        for i in range(0, len(a)):            grad.append((self.cost_function(a_h[i]) - cost_function_at_a) / h)        grad = np.array(grad)        return grad        def update_a(self, learning_rate, grad):        if len(grad) == 1:            grad = grad[0]        self.a -= (learning_rate * grad)        if (self.a_min is not None) or (self.a_min is not None):            self.a = np.clip(self.a, self.a_min, self.a_max)        def update_G(self, grad):        self.G += np.outer(grad,grad.T)        def execute(self, iterations):        for i in range(0, iterations):            self.points.append(list(self.a))            self.result.append(self.cost_function(self.a))            grad = self.grad(self.a)            self.update_a(self.learning_rate, grad)        def execute_adagrad(self, iterations):        for i in range(0, iterations):            self.points.append(list(self.a))            self.result.append(self.cost_function(self.a))            grad = self.grad(self.a)            self.update_G(grad)            learning_rate = self.learning_rate * np.diag(self.G)**(-0.5)            self.update_a(learning_rate, grad)

L’algoritmo viene eseguito per un numero specificato di iterazioni chiamando execute o execute_adagrad. Il metodo execute_adagrad esegue una forma modificata della discesa del gradiente chiamata AdaGrad (discesa del gradiente adattiva).

AdaGrad ha tassi di apprendimento per parametro che aumentano per i parametri sparsi e diminuiscono per i parametri meno sparsi. Il tasso di apprendimento viene aggiornato dopo ogni iterazione in base a una somma storica dei gradienti al quadrato.

Useremo AdaGrad per ottimizzare i guadagni del controllore PID per il sistema di controllo della velocità di crociera dell’auto. Utilizzando AdaGrad, l’equazione di aggiornamento della discesa del gradiente diventa:

Passo di aggiornamento della discesa del gradiente AdaGrad

Ora dobbiamo definire la nostra funzione di costo. La funzione di costo deve prendere come input un vettore di parametri di input e restituire un singolo numero; il costo. L’obiettivo del controllo della velocità di crociera dell’auto è accelerare l’auto fino al valore di velocità impostato con un minimo di sovraelongazione, tempo di stabilizzazione ed errore in regime. Ci sono molti modi in cui potremmo definire la funzione di costo basandoci su questo obiettivo. Qui la definiremo come l’integrale della magnitudine dell’errore nel tempo:

Funzione di costo del controllo della velocità di crociera dell’auto

Dato che la nostra funzione di costo è un integrale, possiamo visualizzarla come l’area sotto la curva di magnitudine dell’errore. Ci aspettiamo di vedere l’area sotto la curva ridursi man mano che ci avviciniamo al minimo globale. Programmatticamente, la funzione di costo è definita come:

def car_cost_function(a):    # Parametri dell'auto    mass = 1000.0  # Massa dell'auto [kg]    Cd = 0.2  # Coefficiente di resistenza all'aria []    Crr = 0.02 # Coefficiente di resistenza al rotolamento []    A = 2.5 # Area frontale dell'auto [m^2]    Fp = 30 # Forza di guida per posizione pedale [%]    # Parametri del controllore PID    Kp = a[0]    Ki = a[1]    Kd = a[2]    # Parametri di simulazione    dt = 0.1  # Passo temporale    total_time = 60.0  # Tempo totale di simulazione    nsteps = int(total_time / dt)    initial_velocity = 0.0  # Velocità iniziale dell'auto [m/s]    target_velocity = 20.0 # Velocità target dell'auto [m/s]    # Definizione degli oggetti Car e PIDController    car = Car(mass, Crr, Cd, A, Fp)    pid_controller = PIDController(Kp, Ki, Kd)    # Esecuzione della simulazione    pedal_s, velocity_s, time = car.simulate(nsteps, dt, initial_velocity, target_velocity, pid_controller)    # Calcolo del costo    cost = np.trapz(np.absolute(target_velocity - velocity_s), time)    return cost

La funzione di costo include i parametri di simulazione. La simulazione viene eseguita per 60 secondi. Durante questo tempo osserviamo la risposta del sistema a un cambiamento a gradino nel setpoint da 0 m/s a 20 m/s. Integrando la magnitudine dell’errore nel tempo, il costo viene calcolato per ogni iterazione.

Ora, tutto ciò che rimane da fare è eseguire l’ottimizzazione. Inizieremo con i valori iniziali di Kp = 5.0, Ki = 1.0 e Kd = 0.0. Questi valori danno una risposta stabile, oscillante, con overshoot, che alla fine converge al setpoint. Da questo punto di partenza eseguiremo l’algoritmo di discesa del gradiente per 500 iterazioni utilizzando un tasso di apprendimento di base di 𝛾=0.1:

a = np.array([5.0, 1.0, 0.0])gradient_descent = GradientDescent(a, 0.1, car_cost_function, a_min=[0,0,0])gradient_descent.execute_adagrad(500)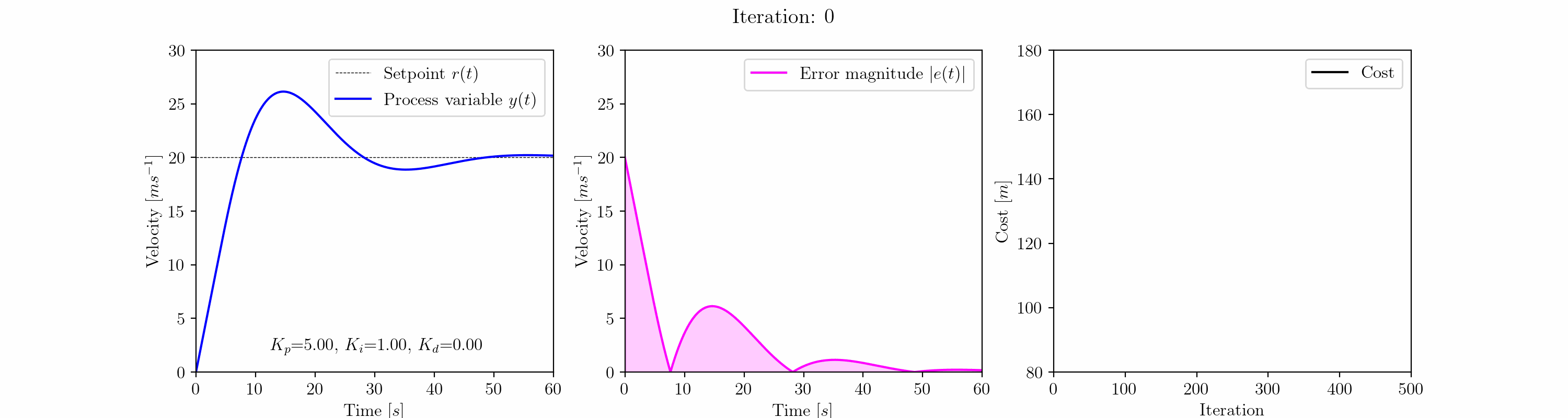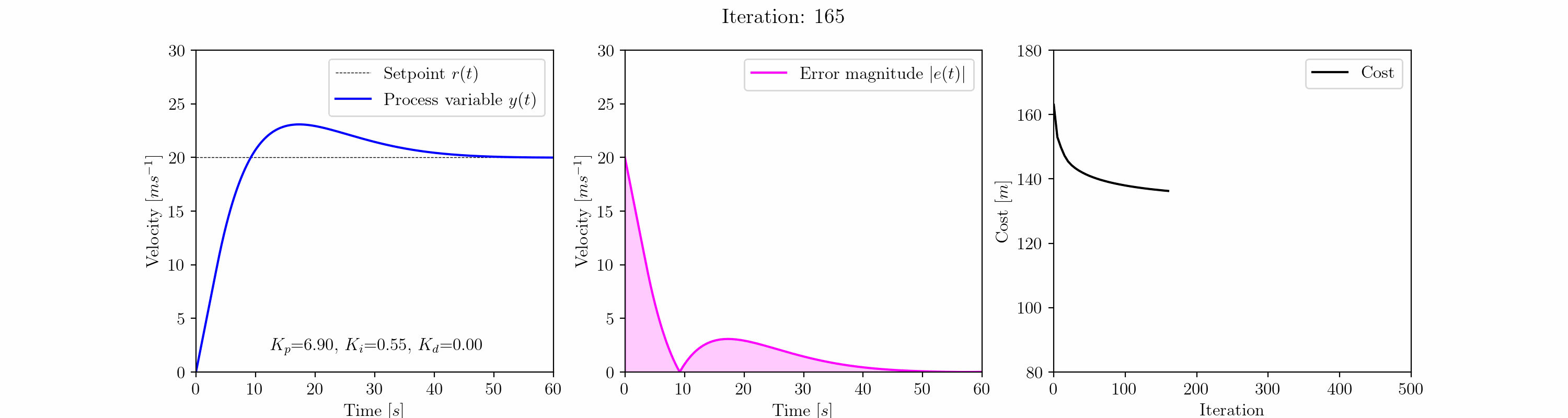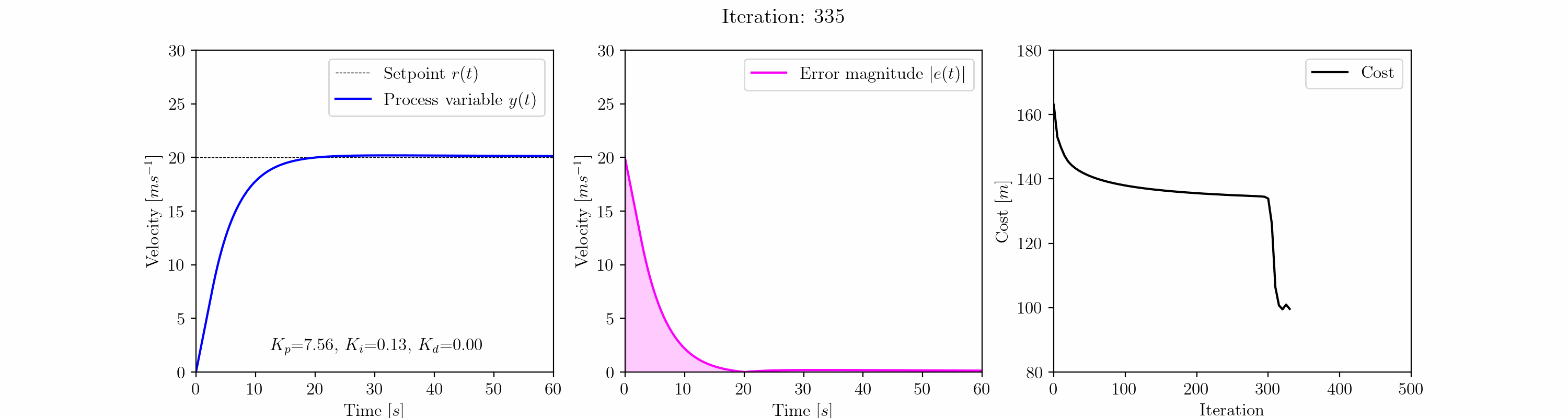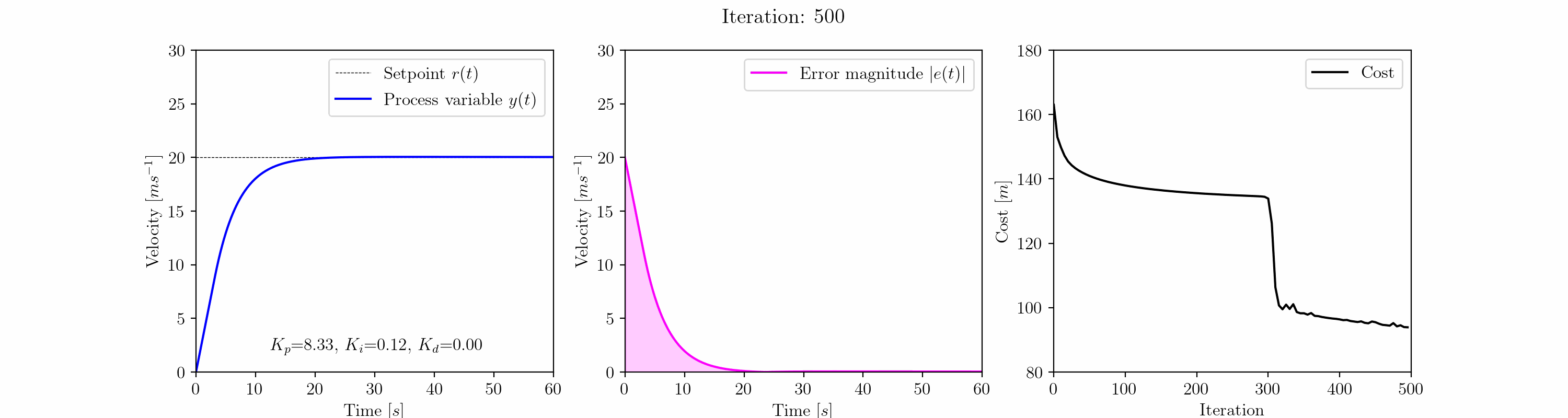

Il grafico animato sopra mostra l’evoluzione della risposta a gradino del controllo di crociera dell’auto mentre l’algoritmo di discesa del gradiente regola i guadagni Kp, Ki e Kd del controllore PID.

All’iterazione 25, l’algoritmo di discesa del gradiente ha eliminato la risposta oscillante. Dopo questo punto, succede qualcosa di interessante. L’algoritmo si imbatte in un minimo locale caratterizzato da un overshoot di ~ 3 m/s. Questo accade nella regione di 6.0 < Kp < 7.5, Ki ~= 0.5, Kd = 0.0 e dura fino all’iterazione 300.

Dopo l’iterazione 300, l’algoritmo esce dal minimo locale per trovare una risposta più soddisfacente più vicina al minimo globale. La risposta è ora caratterizzata da zero overshoot, tempo di stabilizzazione rapido e errore in regime stazionario vicino allo zero.

Eseguendo l’algoritmo di discesa del gradiente per 500 iterazioni arriviamo ai guadagni del controller PID ottimizzato; Kp = 8.33, Ki = 0.12 e Kd = 0.00.

Il guadagno proporzionale sta ancora aumentando costantemente. Eseguendo altre iterazioni (non mostrate qui), mentre Kp aumenta lentamente, troviamo una ulteriore riduzione della funzione di costo che diventa però sempre più marginale.

Sommario

Adottando un metodo ampiamente utilizzato per risolvere problemi di machine learning e deep learning, abbiamo ottimizzato con successo i guadagni del controllore PID per un sistema di controllo di crociera dell’auto.

Iniziando con i valori iniziali di Kp = 5.0, Ki = 1.0 e Kd = 0.0 e applicando la forma AdaGrad dell’algoritmo di discesa del gradiente, abbiamo osservato come questo sistema a bassa dimensione si sia prima imbattuto in un minimo locale per poi trovare una risposta più soddisfacente con zero overshoot, tempo di stabilizzazione rapido e errore in regime stazionario vicino allo zero.

In questo articolo, abbiamo visto come la discesa del gradiente possa essere uno strumento potente quando applicato a problemi di ottimizzazione ingegneristica classica. Oltre all’esempio presentato qui, la discesa del gradiente può essere utilizzata per risolvere altri problemi ingegneristici come la cinematica inversa nella robotica, l’ottimizzazione della topologia e molti altri.

Hai un problema di ottimizzazione a cui pensi che la discesa del gradiente potrebbe essere applicata? Fammelo sapere nei commenti qui sotto.

Ti è piaciuto leggere questo articolo?

Seguimi e iscriviti per altri contenuti come questo – condividilo con la tua rete – prova ad applicare la discesa del gradiente ai tuoi stessi problemi di ottimizzazione.

Tutte le immagini, salvo diversa indicazione, sono dell’autore.

Riferimenti

Web

[1] GitHub (2023), pid_controller_gradient_descent

[2] Wikipedia (2023), Metodo di Ziegler-Nichols (accesso il 10 luglio 2023)