Come limita il principio di incertezza l’analisi delle serie temporali?

Come l'incertezza influenza l'analisi delle serie temporali?

Perché non possiamo estrarre informazioni precise su tempo e frequenza da una serie temporale in modo simultaneo e come l’analisi wavelet può affrontare questa limitazione

1. Introduzione

La connessione tra la Trasformata di Fourier, il Principio di Incertezza e l’analisi delle serie temporali svela un’interazione affascinante che modella l’estrazione di informazioni temporali e di frequenza simultanee. Per comprendere questa relazione, è importante capire brevemente cosa sia una Trasformata di Fourier (FT) e il principio di incertezza come conseguenza. Successivamente, esploriamo la Trasformata Wavelet (WT) come uno strumento promettente per questa limitazione, rivelando specifiche occorrenze temporali di frequenza con chiarezza sufficiente.

1.1 Trasformata di Fourier

La Trasformata di Fourier (FT) funge da ponte matematico tra i domini temporale e di frequenza di una funzione. Una FT può essere descritta come:

Non entrerò nei dettagli di questo integrale, ma la parte importante è che una FT trasforma la funzione f(x) in un’altra funzione g(ω) nello spazio delle frequenze. Conserva quest’informazione per dopo, sarà importante. (Per comprendere meglio la FT, consiglio vivamente il video di 3Blue1Brown.)

• Ingegneria dei dati geospaziali Indicizzazione spaziale
• Google applica filigrane alle immagini generate da intelligenza artificiale per proteggersi dai deepfake
• Questa ricerca sull’IA affronta il problema della ‘perdita di plasticità’ nei sistemi di deep learning quando utilizzati in ambienti di apprendimento continuo

1.2 Principio di Incertezza come conseguenza della Trasformata di Fourier

Nel 1927, il fisico Werner Heisenberg introdusse ciò che probabilmente è uno dei concetti più famosi della meccanica quantistica, il principio di incertezza [1]. Il principio è essenzialmente un teorema sulla Trasformata di Fourier, quando due funzioni sono una Trasformata di Fourier l’una dell’altra, entra in gioco il principio di incertezza.

Mentre momentaneamente tralasciamo la sua intricata fisica, consideriamo solo l’essenza: il prodotto delle incertezze nella posizione x e nell’impulso p rimane limitato. Questa limitazione sottolinea il confine intrinseco nella misurazione di queste quantità con precisione infinita (se sei interessato, guarda questo video).

Questo accade perché la posizione e l’impulso sono una Trasformata di Fourier l’uno dell’altro! Nel caso dell’analisi delle serie temporali, l’analogia della posizione x e dell’impulso p è la serie temporale nello spazio temporale t e di frequenza ω, rispettivamente.

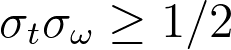
2. Evocare Frequenze con FT nelle Serie Temporali

Una delle applicazioni più importanti della Trasformata di Fourier è nell’analisi delle serie temporali. Considera uno scenario in cui dobbiamo trovare le frequenze intrinseche nella serie temporale. Ad esempio, pensa a distinguere le frequenze prevalenti con cui le persone rivedono un determinato contenuto. Pertanto, vogliamo trasformare f(t) (una serie temporale) in g(ω), una funzione delle frequenze, utilizzando una FT.

2.1 Esempio

Per esemplificare, utilizziamo il dataset dell’anidride carbonica atmosferica settimanale Mauna Loa [2].

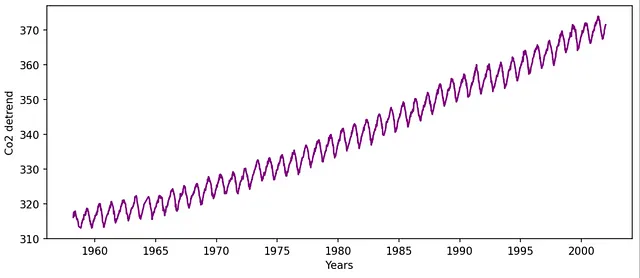
Rimuovere la tendenza lineare per eliminare contributi fasulli a bassa frequenza:

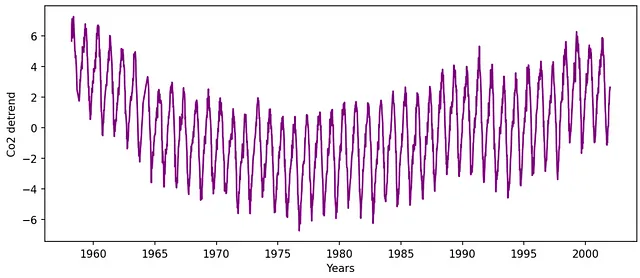
Utilizzando l’algoritmo Fast Fourier Transform (FFT) per calcolare la FT:

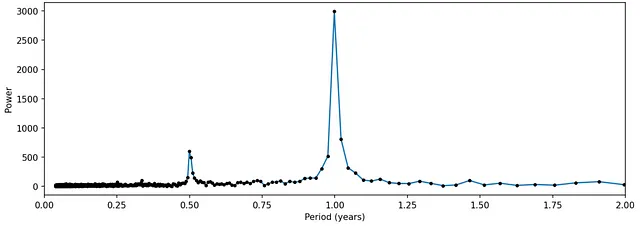
Da qui, è possibile ottenere la frequenza che compone la serie, e in questo caso sono visibili due picchi distinti, uno annuale e l’altro semestrale. Questa è una visualizzazione della chiara stagionalità del dataset.

Tuttavia, gli aspetti più interessanti si verificano quando c’è una perturbazione nella serie temporale, che potrebbe essere l’impatto di un evento o di una variabile esterna (ad esempio, un’eruzione vulcanica vicina). Per simulare ciò, possiamo prendere la stessa serie più un’aggiunta di un seno stocastico:

Applicando la FFT per ottenere la FT della serie:

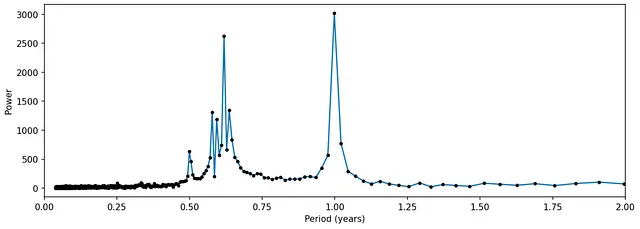
Ora, c’è un altro insieme di picchi tra 0,5 e 0,75 che è causato dalla perturbazione.

2.2 La limitazione

A volte, vogliamo sapere quando è avvenuta la perturbazione e il cambiamento di frequenza, o semplicemente la collocazione temporale di ogni frequenza all’interno della serie. Nella nostra simulazione della serie con e senza perturbazione, è chiaro che la maggior parte dell’impatto avviene all’inizio della serie. Tuttavia, un’ispezione visiva della serie combinata con le informazioni sulla FT non è sufficiente per sapere dove è avvenuta quella perturbazione. Pertanto, abbiamo bisogno di trovare un altro strumento che ci aiuti.

Tuttavia, la Trasformata di Fourier (FT) comporta un compromesso: rimuove le informazioni temporali come mostra il principio di incertezza, rendendoci inconsapevoli di quando queste frequenze si manifestano nella serie. Qui entra in gioco il principio di incertezza. Invece di perseguire una precisione infinita nella frequenza o nel tempo, possiamo sfruttare il principio di incertezza, permettendoci di ottenere approfondimenti su entrambe le quantità con una risoluzione ridotta, mantenendo nel contempo un equilibrio.

3. La Trasformata Wavelet come strumento per il compromesso tra Tempo e Frequenza

La Trasformata Wavelet (WT) emerge come un atto di bilanciamento della risoluzione, che trasforma la nostra funzione f(t) in F(t,ω), una composizione di tempo e frequenza. Non entrerò nei dettagli su come funziona la WT, ma, per riassumere, il processo di trasformazione utilizza una serie di diverse wavelet (segnali con frequenza e forma conosciute) per abbinare la sincronizzazione temporale con la serie temporale attraverso prodotti scalari di due funzioni. Pertanto, è possibile avere un’idea della frequenza e dell’occorrenza temporale, ma limitata da una minore risoluzione in entrambe le quantità.

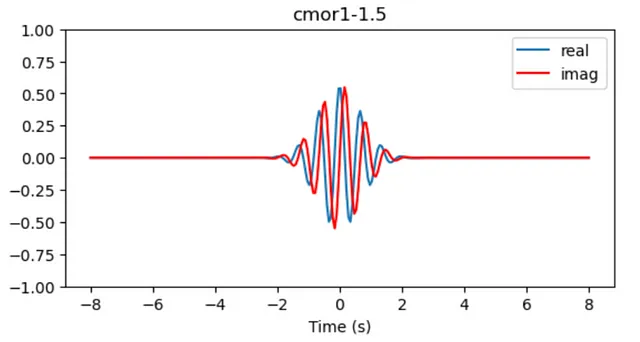
Per visualizzare la trasformata wavelet di un segnale, è comune rappresentare l’asse x come scala temporale e l’asse y come scala di frequenza, e la scala di colore come Potenza della frequenza.

Per la serie temporale senza tendenza senza perturbazioni,

è possibile vedere chiaramente che la stagionalità si ripete negli anni come ci aspettiamo dall’ispezione visiva. Ma il picco enorme della stagionalità di 1 anno dalla Trasformata di Fourier (FT) è ora più ampio, quindi la nostra certezza sul valore è diminuita.

L’analisi più interessante è per lo scenario simulato.

La Trasformata Wavelet mostra che la perturbazione a bassa frequenza osservata nella FT avviene nei primi anni della serie, con conseguenze significative dopo 20-25 anni. Anche se la Trasformata Wavelet perde risoluzione sia nel tempo che nella frequenza, le nuove informazioni sull’occorrenza della frequenza sono preziose e in grado di rispondere a una varietà di domande.

4. Conclusioni

In breve, il Principio di Incertezza impone una limitazione fondamentale all’analisi delle serie temporali, come rivelato dai vincoli della Trasformata di Fourier. Mentre la Trasformata di Fourier estrae efficientemente informazioni di frequenza dai dati delle serie temporali, sacrifica qualsiasi conoscenza su quando si verificano tali frequenze. Pertanto, la Trasformata Wavelet è uno strumento utile che ci permette di bilanciare la risoluzione temporale e quella frequenziale per ottenere approfondimenti sull’occorrenza temporale dei componenti di frequenza accettando un grado di incertezza intrinseco al principio.

Ringraziamenti

Questo incredibile video di Artem Kirsanov mi ha ispirato a scrivere questo articolo. Se desideri approfondire questo argomento, ti consiglio anche di guardare il video.

Osservazioni

• La Trasformata di Fourier (FT) è molto importante non solo per la meccanica quantistica e l’analisi delle serie temporali. Viene utilizzata in questo preciso momento per archiviare i dati di questo articolo in un servizio cloud. Uno degli algoritmi più famosi e utilizzati nella storia si chiama Fast Fourier Transform (FFT) ed è alla base di praticamente ogni compressione dati attuale.
• Per modellare la natura delle particelle subatomiche in modo caratteristico matematico, una Trasformata di Fourier appare naturalmente nella meccanica quantistica. Riflette un cambiamento fondamentale di prospettiva che il principio di incertezza porta alla nostra comprensione della natura. Misurare la posizione di una particella fa perdere informazioni sulla sua velocità e viceversa.

Il notebook per questo articolo è disponibile qui.

Riferimenti

[1] https://en.wikipedia.org/wiki/Uncertainty_principle

[2] https://www.statsmodels.org/dev/datasets/generated/co2.html (dominio pubblico)

[3] Trasformata Wavelet (Wikipedia)