Un’immersione profonda negli Autoencoder e la loro relazione con PCA e SVD.

A deep dive into Autoencoders and their relationship with PCA and SVD.

Un’esplorazione dettagliata degli autoencoder e della riduzione della dimensionalità

Un autoencoder è un tipo di rete neurale che impara a ricostruire il suo input. È composto da una rete encoder che comprime i dati di input in uno spazio a bassa dimensionalità e da una rete decoder che ricostruisce i dati di input da tale spazio. L’encoder e il decoder vengono addestrati congiuntamente per minimizzare l’errore di ricostruzione tra i dati di input e la loro ricostruzione.

Gli autoencoder possono essere utilizzati per varie attività come la compressione di dati, la rimozione del rumore, l’estrazione di caratteristiche, la rilevazione delle anomalie e la modellizzazione generativa. Hanno applicazioni in una vasta gamma di campi come la visione artificiale, l’elaborazione del linguaggio naturale e il riconoscimento vocale. Gli autoencoder possono essere anche utilizzati per la riduzione della dimensionalità. Infatti, uno dei principali scopi degli autoencoder è quello di apprendere una rappresentazione compressa dei dati di input, che può essere utilizzata come forma di riduzione della dimensionalità.

In questo articolo, discuteremo la matematica sottostante agli autoencoder e vedremo come possono fare la riduzione della dimensionalità. Esamineremo anche la relazione tra un autoencoder, l’analisi delle componenti principali (PCA) e la decomposizione ai valori singolari (SVD). Mostreremo anche come implementare sia autoencoder lineari che non lineari in Pytorch.

Architettura dell’autoencoder

• Generazione controllabile di immagini mediche con ControlNets
• NVIDIA RTX sta trasformando i laptop da 14 pollici, oltre alla codifica simultanea dello schermo e il driver May Studio disponibile oggi.
• Una nuova era la serie ‘Age of Empires’ si unisce a GeForce NOW, parte dei 20 giochi in arrivo a giugno.

La figura 1 mostra l’architettura di un autoencoder. Come accennato in precedenza, un autoencoder impara a ricostruire i suoi dati di input, quindi la dimensione dei layer di input e output è sempre la stessa ( n ). Poiché l’autoencoder apprende il proprio input, non richiede dati etichettati per l’addestramento. Pertanto, è un algoritmo di apprendimento non supervisionato.

Ma qual è il punto di apprendere gli stessi dati di input? Come si vede, i layer nascosti in questa architettura sono modellati sotto forma di un imbuto a doppio lato in cui il numero di neuroni in ogni layer diminuisce man mano che ci spostiamo dal primo layer nascosto a un layer che viene definito come il layer bottleneck . Questo layer ha il numero minimo di neuroni. Il numero di neuroni aumenta quindi di nuovo dal layer bottleneck e termina con il layer di output che ha lo stesso numero di nodi del layer di input. È importante notare che il numero di neuroni nel layer bottleneck è inferiore a n .

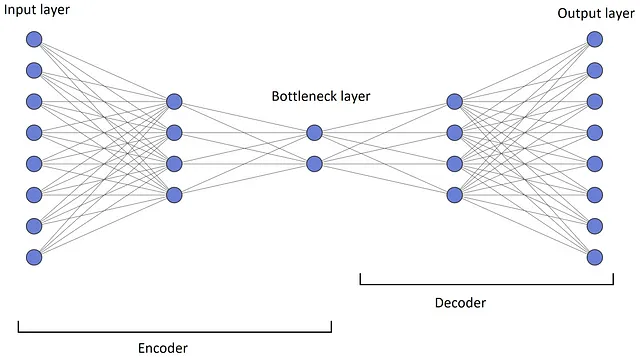
In una rete neurale, ogni layer apprende una rappresentazione astratta dello spazio di input, quindi il layer bottleneck è effettivamente un collo di bottiglia per le informazioni che si trasferiscono tra i layer di input e output. Questo layer impara la rappresentazione più compatta dei dati di input rispetto agli altri layer e impara anche ad estrarre le caratteristiche più importanti dei dati di input. Queste nuove caratteristiche (chiamate anche variabili latenti ) sono il risultato della trasformazione dei punti dati di input in uno spazio continuo a bassa dimensionalità. Infatti, le variabili latenti possono descrivere o spiegare i dati di input in modo più semplice. L’output dei neuroni nel layer bottleneck rappresenta i valori di queste variabili latenti.

La presenza di un layer bottleneck è la caratteristica chiave di questa architettura. Se tutti i layer nella rete avessero lo stesso numero di neuroni, la rete potrebbe facilmente imparare a memorizzare i valori dei dati di input passandoli tutti lungo la rete.

Un autoencoder può essere diviso in due reti:

1. Rete encoder: inizia dal layer di input e termina al layer bottleneck. Trasforma i dati di input ad alta dimensionalità nello spazio a bassa dimensionalità formato dalle variabili latenti. L’output dei neuroni nel layer bottleneck rappresenta i valori di queste variabili latenti.
2. Rete decoder: inizia dopo il layer bottleneck e termina al layer di output. Riceve i valori delle variabili latenti a bassa dimensionalità dal layer bottleneck e ricostruisce i dati di input ad alta dimensionalità originali da essi.

In questo articolo, discuteremo la somiglianza tra gli autoencoder e la PCA. Per comprendere la PCA, abbiamo bisogno di alcuni concetti di algebra lineare. Quindi, prima rivediamo l’algebra lineare.

Rivisitazione dell’algebra lineare: Base, dimensione e rango

Un insieme di vettori { v ₁, v ₂, …, v_ n } forma una base dello spazio vettoriale V, se essi sono linearmente indipendenti e generano V. Se un insieme di vettori è linearmente indipendente, allora nessun vettore dell’insieme può essere scritto come una combinazione lineare degli altri vettori. Un insieme di vettori { v ₁, v ₂, …, v_ n } genera uno spazio vettoriale se ogni altro vettore in tale spazio può essere scritto come una combinazione lineare di questo insieme. Quindi, ogni vettore x in V può essere scritto come:

dove a ₁, a ₂, …, a_n sono alcune costanti. Lo spazio vettoriale V può avere molte diverse basi di vettori, ma ogni base ha sempre lo stesso numero di vettori. Il numero di vettori in una base di uno spazio vettoriale è chiamato la sua dimensione. Una base { v ₁, v ₂, …, v_ n } è ortonormale quando tutti i vettori sono normalizzati (la lunghezza di un vettore normalizzato è 1) e ortogonali (mutuamente perpendicolari). Nello spazio euclideo R², i vettori:

formano una base ortonormale chiamata base standard. Sono linearmente indipendenti e generano tutti i vettori in R². Poiché la base ha solo due vettori, la dimensione di R² è 2. Se abbiamo un’altra coppia di vettori che sono linearmente indipendenti e generano R², quella coppia può anche essere una base per R². Ad esempio:

è anche una base, ma non è una base ortonormale poiché i vettori non sono ortogonali. In generale, possiamo definire la base standard per R^ n come:

dove in e ᵢ l’i-esimo elemento è uno e tutti gli altri elementi sono zero.

Lasciamo che l’insieme di vettori B = { v ₁, v ₂, …, v_ n } formi una base per uno spazio vettoriale, quindi possiamo scrivere qualsiasi vettore x in tale spazio in termini dei vettori della base:

Quindi le coordinate di x rispetto a questa base B possono essere scritte come:

In realtà, quando definiamo un vettore in R² come:

gli elementi di questo vettore sono le sue coordinate rispetto alla base standard:

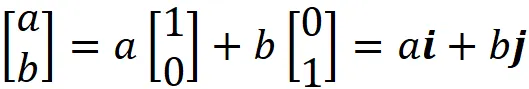
Possiamo facilmente trovare le coordinate di un vettore rispetto a un’altra base. Supponiamo di avere il vettore:

dove B ={ v ₁, v ₂, …, v_ n } è una base. Ora possiamo scrivere:

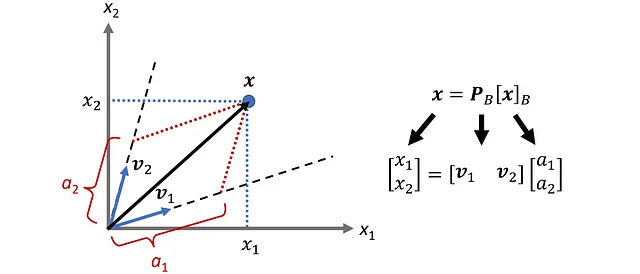
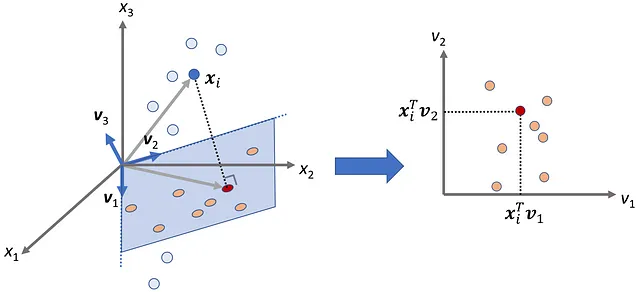
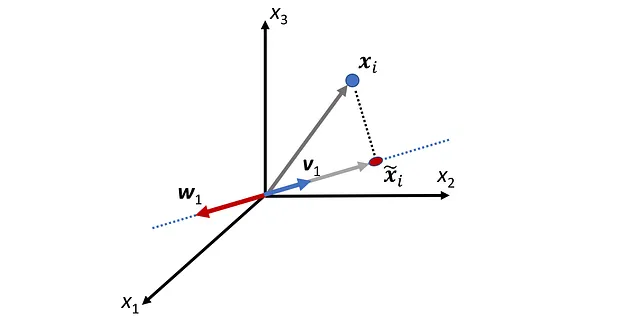
Qui P_ B è chiamata matrice di cambio di coordinate e le sue colonne sono i vettori nella base B . Quindi, se abbiamo le coordinate di x relative alla base B , possiamo calcolare le sue coordinate relative alla base standard utilizzando l’Equazione 1. La Figura 2 mostra un esempio. Qui la B ={ v ₁, v ₂} è una base per R². Il vettore x è definito come:

E le coordinate di x relative a B sono:

Quindi, abbiamo:

Lo spazio colonna della matrice A (scritto anche come Col A ) è l’insieme di tutte le combinazioni lineari delle colonne di A . Supponiamo che le colonne della matrice A siano indicate dai vettori a ₁ , a ₂ , … a_ n . Ora, per qualsiasi vettore come u , Au può essere scritto come:

Quindi, Au è una combinazione lineare delle colonne di A , e lo spazio colonna di A è l’insieme di vettori che possono essere scritti come Au .

Lo spazio riga di una matrice A è l’insieme di tutte le combinazioni lineari delle righe di A . Supponiamo che le righe della matrice A siano indicate dai vettori a ₁ ᵀ, a ₂ ᵀ, … a_m ᵀ:

Lo spazio riga di A è l’insieme di tutti i vettori che possono essere scritti come

Il numero di vettori di base di Col A o la dimensione di Col A è chiamato rango di A . Il rango di A è anche il numero massimo di colonne linearmente indipendenti di A . Si può anche dimostrare che il rango di una matrice A è uguale alla dimensione del suo spazio riga, e allo stesso modo, è uguale al numero massimo di righe linearmente indipendenti di A . Quindi, il rango di una matrice non può superare il numero delle sue righe o colonne. Ad esempio, per una matrice m × n, il rango non può essere maggiore di min ( m , n ).

PCA: una recensione

L’analisi delle componenti principali (PCA) è una tecnica lineare. Trova le direzioni dei dati che catturano la maggior variazione e quindi proietta i dati su uno spazio di dimensioni inferiori spaziato da queste direzioni. La PCA è un metodo ampiamente utilizzato per ridurre la dimensionalità dei dati.

La PCA trasforma i dati in un nuovo sistema di coordinate ortogonale. Questo sistema di coordinate è scelto in modo tale che la varianza dei punti dati proiettati sull’asse delle coordinate principali (chiamato il primo componente principale) sia massimizzata. La varianza dei punti dati proiettati sull’asse delle coordinate secondarie (chiamato il secondo componente principale) è massimizzata tra tutte le possibili direzioni ortogonali al primo componente principale e, in generale, la varianza dei punti dati proiettati su ogni asse delle coordinate è massimizzata tra tutte le possibili direzioni ortogonali ai componenti principali precedenti.

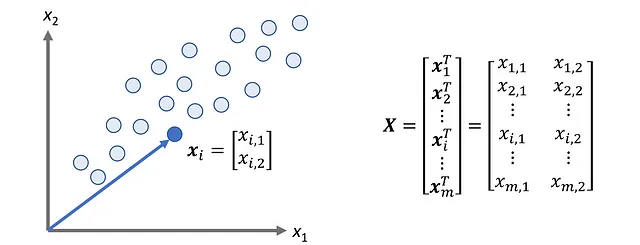
Supponiamo di avere un set di dati con n caratteristiche e m punti dati o osservazioni. Possiamo utilizzare la matrice m × n

per rappresentare questo set di dati e lo chiamiamo matrice di progetto. Quindi ogni riga di X rappresenta un punto dati e ogni colonna rappresenta una caratteristica. Possiamo anche scrivere X come

dove ogni vettore colonna

rappresenta un’osservazione (o punto dati) in questo set di dati. Quindi, possiamo pensare al nostro set di dati come a un insieme di vettori m in R^n. Figura 3 mostra un esempio per n =2. Qui possiamo rappresentare ogni osservazione come un vettore (o semplicemente un punto) in R².

Sia u un vettore unitario, quindi abbiamo:

La proiezione scalare di ogni punto dati xᵢ sul vettore u è:

Figura 4 mostra un esempio per n =2.

Indichiamo con m la media di ogni colonna di X:

Quindi la media del set di dati può essere definita come:

E possiamo anche scriverlo come:

Ora la varianza di questi punti dati proiettati è definita come:

L’Equazione 1 può essere ulteriormente semplificata. Il termine

è uno scalare (poiché il risultato di a è una quantità scalare). Inoltre, sappiamo che la trasposizione di una quantità scalare è uguale a se stessa. Quindi, possiamo avere

Quindi, la varianza della proiezione scalare dei punti dati in X sul vettore u può essere scritta come

dove

è chiamata matrice di covarianza (Figura 5).

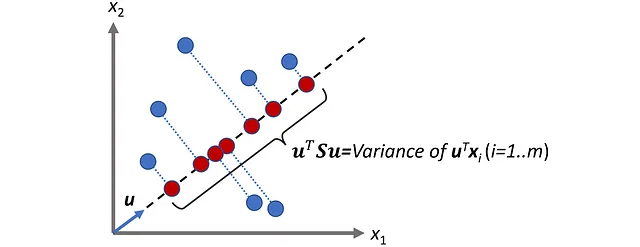
Semplificando l’Equazione 5, si può dimostrare che la matrice di covarianza può essere scritta come:

dove

Qui xᵢ, ₖ è l’elemento (i, k) della matrice di progettazione X (o semplicemente l’elemento k-esimo del vettore xᵢ).

Per un dataset con n caratteristiche, la matrice di covarianza è una matrice n × n. Inoltre, basandoci sulla definizione di Sᵢ,ⱼ nell’Equazione 6, abbiamo:

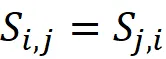
Quindi, il suo elemento (i, j) è uguale al suo elemento (j, i), il che significa che la matrice di covarianza è una matrice simmetrica ed è uguale alla sua trasposta:

Ora troviamo il vettore u₁ che massimizza

Poiché u₁ è un vettore normalizzato, aggiungiamo questo vincolo al problema di ottimizzazione:

Possiamo risolvere questo problema di ottimizzazione aggiungendo il moltiplicatore di Lagrange λ₁ e massimizzando

Per farlo, poniamo la derivata di questo termine rispetto a u₁ uguale a zero:

E otteniamo:

Ciò significa che u ₁ è un autovettore della matrice di covarianza S, e λ ₁ è il suo corrispondente autovalore. Chiamiamo l’autovettore u ₁ il primo componente principale. Successivamente, vogliamo trovare il vettore unitario u ₂ che massimizza u ₂ᵀ Su ₂ tra tutte le possibili direzioni ortogonali al primo componente principale. Quindi, dobbiamo trovare il vettore u ₂ che massimizza u ₂ ᵀ Su ₂ con queste restrizioni:

Si può dimostrare che u ₂ è la soluzione di questa equazione:

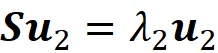
Concludiamo quindi che u ₂ è anche un autovettore di S, e λ ₂ è il suo corrispondente autovalore (la dimostrazione è data in appendice). Più in generale, vogliamo trovare il vettore unitario u ᵢ che massimizza u ᵢᵀ Su ᵢ tra tutte le possibili direzioni ortogonali ai precedenti componenti principali u ₁… u_ i -1. Pertanto, dobbiamo trovare il vettore u ᵢ che massimizza

con queste restrizioni:

Anche in questo caso si può dimostrare che u ᵢ è la soluzione di questa equazione:

Pertanto, u ᵢ è un autovettore di S, e λᵢ è il suo corrispondente autovalore (la dimostrazione è data in appendice). Il vettore u ᵢ è chiamato l’i-esimo componente principale. Se abbiamo un dataset con n caratteristiche, la matrice di covarianza sarà una matrice simmetrica n × n. Qui ogni punto dati può essere rappresentato da un vettore in R^ n (xᵢ). Come già detto, gli elementi di un vettore in R^ n danno le sue coordinate relative alla base standard.

È possibile dimostrare che una matrice simmetrica n × n ha n autovalori reali e n autovettori corrispondenti linearmente indipendenti e ortogonali (teorema spettrale). Questi n autovettori ortogonali sono le componenti principali di questo dataset. È possibile dimostrare che un insieme di n vettori ortogonali può formare una base per R^n. Quindi, queste componenti principali formano una base ortogonale e possono essere utilizzate per definire un nuovo sistema di coordinate per i punti dati (Figura 6).

Possiamo facilmente calcolare le coordinate di ogni punto dati x ᵢ rispetto a questo nuovo sistema di coordinate. Sia B = {v ₁, v ₂, …, v_ n} l’insieme delle componenti principali. Scriviamo prima x ᵢ in termini dei vettori della base:

Ora, se moltiplichiamo entrambi i lati di questa equazione per v ᵢᵀ otteniamo:

Dato che abbiamo una base ortogonale:

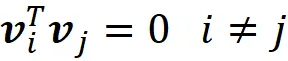
Quindi segue che

Dato che il prodotto scalare è commutativo, possiamo anche scrivere:

Quindi, le coordinate di x ᵢ rispetto a B sono:

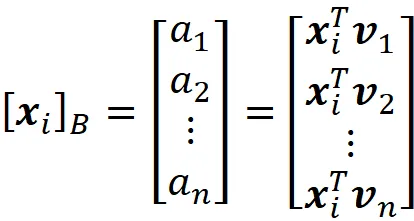
e la matrice di progetto può essere scritta come

nel nuovo sistema di coordinate. Qui ogni riga rappresenta un punto dati (osservazione) nel nuovo sistema di coordinate. La Figura 6 mostra un esempio per n = 2.

La varianza della proiezione scalare dei punti dati su ciascun autovettore (componente principale) è uguale al suo corrispondente autovalore. La prima componente principale ha la maggiore autovalore (varianza). La seconda componente principale ha il secondo maggiore autovalore e così via. Ora possiamo scegliere le prime d componenti principali e proiettare i punti dati originali sul sottospazio da esse generato.

Quindi, trasformiamo i punti dati originali (con n caratteristiche) in questi punti dati proiettati che appartengono a un sottospazio di dimensione d. In questo modo, riduciamo la dimensionalità del dataset originale da n a d, massimizzando la varianza dei dati proiettati. Ora le prime d colonne della matrice nell’Equazione 9 danno le coordinate dei punti dati proiettati:

La Figura 7 mostra un esempio di questa trasformazione. Il dataset originale ha 3 caratteristiche (n = 3) e riduciamo la sua dimensionalità a d = 2 proiettando i punti dati sul piano formato dalle prime due componenti principali (v ₁, v ₂). Le coordinate di ogni punto dati x ᵢ nel sottospazio generato da v ₁ e v ₂ sono:

È consueto centrare il dataset intorno allo zero prima dell’analisi PCA. Per fare ciò, prima creiamo la matrice di progetto X che rappresenta il nostro dataset (Equazione 2). Quindi creiamo una nuova matrice Y sottraendo la media di ogni colonna dagli elementi in quella colonna

La matrice Y rappresenta il dataset centrato. In questa nuova matrice, la media di ogni colonna è zero:

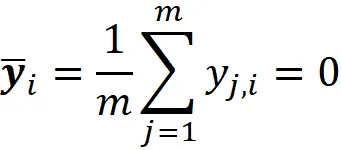
Quindi, la media del dataset è anche zero:

Ora supponiamo di partire da una matrice di progetto centrata X e di voler calcolare la sua matrice di covarianza. Quindi, la media di ogni colonna di X è zero. Dall’Equazione 6 abbiamo:

dove [ X ]_ k , j denota l’elemento ( k , j ) della matrice X . Utilizzando la definizione di moltiplicazione di matrici, otteniamo

Si prega di notare che questa equazione è valida solo quando la matrice di progetto ( X ) è centrata.

La relazione tra PCA e scomposizione in valori singolari (SVD)

Supponiamo che A sia una matrice m × n. Quindi A ᵀ A sarà una matrice quadrata n × n, ed è facile dimostrare che è una matrice simmetrica. Poiché A ᵀ A è simmetrica, ha n autovalori reali e n autovettori linearmente indipendenti e ortogonali (teorema spettrale). Chiamiamo questi autovettori v ₁, v ₂, …, v_ n e assumiamo che siano normalizzati. Si può dimostrare che gli autovalori di A ᵀ A sono tutti positivi. Ora supponiamo di etichettarli in ordine decrescente, quindi:

Sia v ₁, v ₂, …, v_ n gli autovettori di A ᵀ A corrispondenti a questi autovalori. Definiamo il valore singolare della matrice A (denotato da σᵢ ) come la radice quadrata di λᵢ . Quindi abbiamo

Ora supponiamo che il rango di A sia r . Quindi si può dimostrare che il numero di autovalori non nulli di A ᵀ A o il numero di valori singolari non nulli di A è r:

Ora la decomposizione ai valori singolari (SVD) di A può essere scritta come

Qui V è una matrice n×n e le sue colonne sono v ᵢ :

Σ è una matrice diagonale di m × n, e tutti gli elementi di Σ sono nulli tranne i primi r elementi diagonali che sono uguali ai valori singolari di A . Definiamo la matrice U come

Definiamo u ₁ fino a u_ r come

Possiamo facilmente dimostrare che questi vettori sono ortogonali:

Qui abbiamo usato il fatto che v_ j è un autovettore di A ᵀ A e questi autovettori sono ortogonali. Poiché questi vettori sono ortogonali, sono anche linearmente indipendenti. Gli altri vettori u ᵢ ( r<i≤m ) sono definiti in modo che u ₁, u ₂, … u _m formino una base per uno spazio vettoriale di m dimensioni ( R^ m) .

Sia X una matrice di progetto centrata, e la sua decomposizione SVD è la seguente:

Come già detto, v ₁, v ₂, …, v_ n sono gli autovettori di X ᵀ X e i valori singolari sono la radice quadrata dei loro corrispondenti autovalori. Quindi, abbiamo

Ora possiamo dividere entrambi i lati dell’equazione precedente per m (dove m è il numero di punti dati) e usare l’Equazione 10, per ottenere

Quindi, si segue che v ᵢ è l’autovettore della matrice di covarianza e il suo autovalore corrispondente è il quadrato del suo valore singolare corrispondente diviso m . Quindi, la matrice V nell’equazione SVD fornisce le componenti principali di X, e utilizzando i valori singolari in Σ , possiamo facilmente calcolare gli autovalori. In sintesi, possiamo usare SVD per fare PCA.

Vediamo cos’altro possiamo ottenere dall’equazione SVD. Possiamo semplificare UΣ nell’Equazione 12 usando le Equazioni 3 e 11:

Confrontando con l’Equazione 9, si conclude che l’i-esima riga di UΣ fornisce le coordinate del punto dati x ᵢ rispetto alla base definita dai componenti principali.

Ora supponiamo che nell’Equazione 12, manteniamo solo le prime k colonne di U, le prime k righe di V e le prime k righe e colonne di Σ. Se le moltiplichiamo insieme, otteniamo:

Si prega di notare che X ₖ è ancora una matrice m × n. Se moltiplichiamo X ₖ per il vettore b che ha n elementi, otteniamo:

dove [ Cb ] ᵢ è l’i-esimo elemento del vettore Cb. Dal momento che u ₁, u ₂, …, u ₖ sono vettori linearmente indipendenti (ricorda che formano una base, quindi dovrebbero essere linearmente indipendenti) e che spaziano X ₖ b, si conclude che formano una base per X ₖ b. Questa base ha k vettori, quindi la dimensione dello spazio colonna di X ₖ è k. Pertanto X ₖ è una matrice di rango k.

Ma cosa rappresenta X ₖ? Usando l’Equazione 13 possiamo scrivere:

Quindi, l’i-esima riga di X ₖ è la trasposizione di:

che è la proiezione vettoriale del punto dati x ᵢ sul sottospazio spaziato dai componenti principali v ₁, v ₂, … v ₖ. Ricorda che v ₁, v ₂, … v_ n è una base per il nostro dataset originale. Inoltre, le coordinate di x ᵢ relative a questa base sono:

Pertanto, usando l’Equazione 1, possiamo scrivere x ᵢ come:

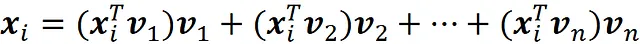
Ora possiamo scomporre x ᵢ in due vettori. Uno è nello spazio definito dai vettori definiti da v ₁, v ₂, … v ₖ, e l’altro nello spazio definito dagli altri vettori.

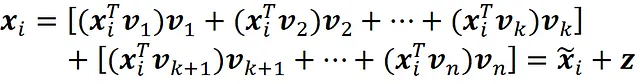
Il primo vettore è il risultato della proiezione di x ᵢ sul sottospazio definito dai vettori definiti da v ₁, v ₂, … v ₖ ed è uguale a x̃ ᵢ.

Ricorda che ogni riga della matrice di progetto X rappresenta uno dei punti dati originali. Allo stesso modo, ogni riga di X ₖ rappresenta lo stesso punto dati proiettato sul sottospazio generato dai componenti principali v ₁, v ₂, … v ₖ (Figura 8).

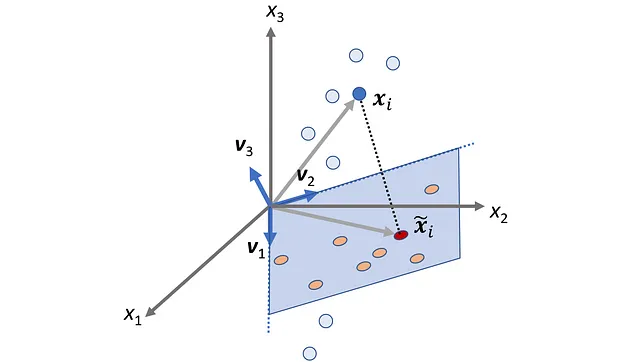
Ora possiamo calcolare la distanza tra il punto dati originale ( x ᵢ ) e il punto dati proiettato ( x̃ ᵢ ). Il quadrato della distanza tra i vettori x ᵢ e x̃ᵢ è:

E se aggiungiamo il quadrato delle distanze per tutti i punti dati, otteniamo:

La norma di Frobenius di una matrice m × n C è definita come:

Dato che i vettori x ᵢ e x̃ ᵢ sono la trasposizione delle righe delle matrici X e X ₖ , possiamo scrivere:

Quindi, la norma di Frobenius di X – X ₖ è proporzionale alla somma del quadrato delle distanze tra i punti dati originali e i punti dati proiettati (Figura 9), e poiché i punti dati proiettati si avvicinano ai punti dati originali, || X – X ₖ ||_ F diminuisce.

Vogliamo che i punti proiettati siano una buona approssimazione dei punti dati originali, quindi vogliamo che X ₖ dia il valore più basso per X – X ₖ tra tutte le matrici di rango k.

Supponiamo di avere la matrice m × n X con rango = r e i valori singolari di X sono ordinati, quindi abbiamo:

Si può dimostrare che X ₖ minimizza la norma di Frobenius di X – A tra tutte le matrici m × n A che hanno un rango di k . Matematicamente:

X ₖ è la matrice più vicina a X tra tutte le matrici di rango k e può essere considerata come la migliore approssimazione di rango k della matrice di progetto X . Ciò significa anche che i punti dati proiettati rappresentati da X ₖ sono la migliore approssimazione di rango k (in termini di errore totale) per i punti dati originali rappresentati da X .

Ora possiamo provare a scrivere l’equazione precedente in un formato diverso. Supponiamo che Z sia una matrice m × k e W sia una matrice k × n. Possiamo dimostrare che

Quindi trovare una matrice di rango k A che minimizza || X – A ||_F è equivalente a trovare le matrici Z e W che minimizzano || X – ZW ||_F (la prova è data in appendice). Pertanto, possiamo scrivere

dove Z * (una matrice m × k ) e W * (una matrice k × n) sono le soluzioni al problema di minimizzazione e abbiamo

Ora, basandoci sulle equazioni 13 e 14, possiamo scrivere:

Quindi, se risolviamo il problema di minimizzazione nell’Equazione 18 utilizzando SVD, otteniamo i seguenti valori per Z * e W *:

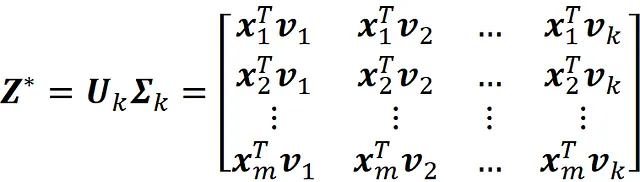
e

Le righe di W * danno la trasposta dei componenti principali e le righe di Z * danno la trasposta delle coordinate di ogni punto dati proiettato rispetto alla base formata da questi componenti principali. È importante notare che i componenti principali formano una base ortogonale (quindi i componenti principali sono sia normalizzati che ortogonali). Infatti, possiamo assumere che la PCA cerchi solo una matrice W in cui le righe formano un insieme ortogonale. Sappiamo che quando due vettori sono ortogonali, il loro prodotto interno è zero, quindi possiamo dire che la PCA (o SVD) risolve il problema di minimizzazione

con questo vincolo:

dove Z e W sono matrici m × k e k × n. Inoltre, se Z * e W * sono le soluzioni al problema di minimizzazione, allora abbiamo

Questa formulazione è molto importante poiché ci permette di stabilire una connessione tra PCA e autoencoder.

La relazione tra PCA e autoencoder

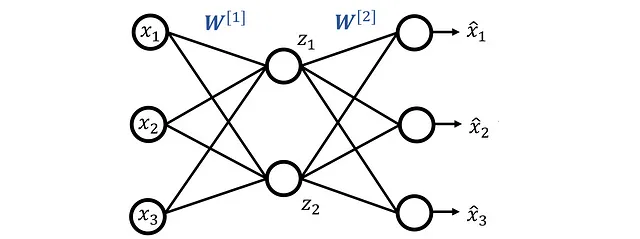
Partiamo da un autoencoder che ha solo tre strati e viene mostrato in figura 10. Questa rete ha n funzionalità di input indicate da x ₁ … x_n e n neuroni al livello di output. Le uscite della rete sono indicate da x^ ₁… x^_n . Il livello nascosto ha k neuroni (dove k < n ) e le uscite del livello nascosto sono indicate da z ₁… zₖ . Le matrici W^ [1] e W^ [2] contengono i pesi del livello nascosto e del livello di output rispettivamente.

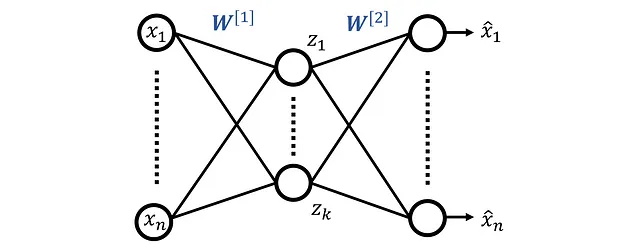
Qui

rappresenta il peso per l’input j-esimo (proveniente dal j-esimo neurone nel layer l-1) dell’i-esimo neurone nel layer l (Figura 11). Qui assumiamo che per il livello nascosto l=1 e per il layer di output l=2.

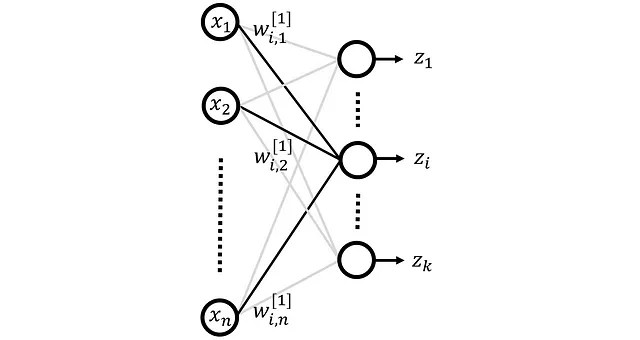
Quindi i pesi del layer nascosto sono dati da:

E la riga i-esima di questa matrice fornisce tutti i pesi dell’i-esimo neurone nel layer nascosto. Allo stesso modo, i pesi del layer di output sono dati da:

Ogni neurone ha una funzione di attivazione. Possiamo calcolare l’output di un neurone nel layer nascosto (attivazione di quel neurone) usando la matrice dei pesi W^ [1] e le caratteristiche di input:

Dove bᵢ ^[1] è il bias per l’i-esimo neurone, e g^ [1] è la funzione di attivazione dei neuroni nel layer 1. Possiamo scrivere questa equazione in forma vettoriale come:

dove b è il vettore di bias:

e x è il vettore delle caratteristiche di input:

Allo stesso modo, possiamo scrivere l’output dell’i-esimo neurone nel layer di output come:

E in forma vettoriale, diventa:

Ora supponiamo di utilizzare la seguente matrice di progettazione come set di dati di formazione per allenare questa rete:

Quindi il set di dati di formazione ha m osservazioni (esempi) e n caratteristiche. Ricorda che l’i-esima osservazione è rappresentata dal vettore

Se alimentiamo questo vettore nella rete, l’output della rete è indicato da questo vettore:

Dobbiamo anche fare le seguenti ipotesi per assicurare che l’autoencoder imiti la PCA:

1-Il dataset di training è centrato, quindi la media di ogni colonna di X è zero:

2-L’attivazione delle funzioni del livello nascosto e di output è lineare e il bias di tutti i neuroni è zero. Ciò significa che stiamo usando un codificatore e un decodificatore lineare in questa rete. Quindi abbiamo:

3-Usiamo la funzione di perdita quadratica per addestrare questa rete. Quindi la funzione di costo è l’errore quadratico medio (MSE) e viene definita come:

Ora possiamo dimostrare che:

dove Z è definito come:

La dimostrazione è data nell’appendice. Qui, l’i-esima riga di Z fornisce l’output del livello nascosto quando l’i-esima osservazione viene alimentata nella rete. Pertanto, minimizzare la funzione di costo di questa rete è lo stesso che minimizzare:

dove definiamo la matrice W come

Si prega di notare che ogni riga di W ^[2] è una colonna di W .

Sappiamo che se moltiplichiamo una funzione con un moltiplicatore positivo, il suo minimo non cambia. Quindi possiamo rimuovere il moltiplicatore 1/(2 m ) quando minimizziamo la funzione di costo. Quindi addestrando questa rete, stiamo risolvendo questo problema di minimizzazione:

dove Z e W sono matrici m × k e k × n. Se confrontiamo questa equazione con l’Equazione 20, vediamo che è lo stesso problema di minimizzazione della PCA. Pertanto, la soluzione dovrebbe essere la stessa di quella dell’Equazione 20:

Tuttavia, qui abbiamo una differenza importante. Il vincolo dell’Equazione 21 non viene applicato qui. Quindi ecco la domanda. I valori ottimali di Z e W trovati dall’autoencoder sono gli stessi di quelli della PCA? Le righe di W * dovrebbero sempre formare un insieme ortogonale?

Per prima cosa, espandiamo l’equazione precedente.

Sappiamo che la i-esima riga di X ₖ è la trasposta di:

che è la proiezione vettoriale del punto dati x ᵢ sul sottospazio generato dai componenti principali v ₁, v ₂, … v ₖ . Quindi, x̃ ᵢ appartiene a un sottospazio k-dimensionale. I vettori w ₁, w ₂, … w ₖ devono essere linearmente indipendenti. In caso contrario, il rango di W * sarà inferiore a k (ricorda che il rango di W * è uguale al numero massimo di righe linearmente indipendenti di W *), e in base all’Equazione A.3 il rango di X ₖ sarà inferiore a k. Si può dimostrare che un insieme di k vettori linearmente indipendenti formano una base per un sottospazio k-dimensionale. Perciò, concludiamo che i vettori w ₁, w ₂, … w ₖ formano anche una base per lo stesso sottospazio generato dai componenti principali. Possiamo ora usare l’Equazione 24 per scrivere la i-esima riga di X ₖ in termini dei vettori w ₁, w ₂, … w ₖ .

Ciò significa che la i-esima riga di Z * fornisce semplicemente le coordinate di x̃ ᵢ rispetto alla base formata dai vettori w ₁, w ₂, … w ₖ . La Figura 12 mostra un esempio con k =2.

In sintesi, le matrici Z * e W * trovate dall’autoencoder possono generare lo stesso sottospazio generato dai componenti principali. Otteniamo anche gli stessi punti dati proiettati di PCA poiché:

Tuttavia, queste matrici definiscono una nuova base per quel sottospazio. A differenza dei componenti principali trovati da PCA, i vettori di questa nuova base non sono necessariamente ortogonali. Le righe di W * danno la trasposta dei vettori della nuova base e le righe di Z * danno la trasposta delle coordinate di ogni punto dati rispetto a quella base.

Concludiamo quindi che un autoencoder lineare non può trovare il componente principale, ma può trovare il sottospazio generato da essi usando una base diversa. C’è un’eccezione qui.. Supponiamo che vogliamo mantenere solo il primo componente principale v ₁. Quindi vogliamo ridurre la dimensionalità del dataset originale da n a 1. In questo caso, il sottospazio è solo una linea retta generata dal primo componente principale. Un autoencoder lineare troverà anche la stessa linea con un vettore di base diverso w ₁. Questo vettore di base non è necessariamente normalizzato e potrebbe avere la direzione opposta di v ₁, ma si trova comunque sulla stessa linea (sottospazio). Questo è dimostrato nella Figura 13. Ora, se normalizziamo w ₁, otteniamo il primo componente principale del dataset. Quindi in questo caso, un autoencoder lineare è in grado di trovare il primo componente principale in modo indiretto.

Fino ad ora, abbiamo discusso della teoria che sta alla base degli autoencoder e del PCA. Ora vediamo un esempio in Python. Nella prossima sezione creeremo un autoencoder usando Pytorch e lo compareremo con il PCA.

Caso di studio: PCA vs autoencoder

Prima di tutto, dobbiamo creare un dataset. Il codice Listing 1 crea un dataset semplice con 3 caratteristiche. Le prime due caratteristiche ( x ₁ e x ₂) hanno una distribuzione normale multivariata 2d e la terza caratteristica ( x ₃) è uguale alla metà di x ₂. Questo dataset è memorizzato nell’array X che gioca il ruolo della matrice di progetto. Inoltre, centriamo la matrice di progetto.

# Codice Listing 1import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom sklearn.decomposition import PCAfrom scipy.stats import multivariate_normalimport torchimport torch.nn as nnfrom numpy import linalg as LAfrom sklearn.preprocessing import MinMaxScalerimport random%matplotlib inlinenp.random.seed(1)mu = [0, 0]Sigma = [[1, 1],         [1, 2.5]]         # X è la matrice di progetto e ogni riga di X è un esempioX = np.random.multivariate_normal(mu, Sigma, 10000)X = np.concatenate([X, X[:, 0].reshape(len(X), 1)], axis=1)X[:, 2] = X[:, 1] / 2X = (X - X.mean(axis=0))x, y, z = X.T

Il codice Listing 2 crea un grafico 3d di questo dataset e il risultato è mostrato nella Figura 14.

# Codice Listing 2fig = plt.figure(figsize=(10, 10))ax1 = fig.add_subplot(111, projection='3d')ax1.scatter(x, y, z, color = 'blue')ax1.view_init(20, 185)ax1.set_xlabel("$x_1$", fontsize=20)ax1.set_ylabel("$x_2$", fontsize=20)ax1.set_zlabel("$x_3$", fontsize=20)ax1.set_xlim([-5, 5])ax1.set_ylim([-7, 7])ax1.set_zlim([-4, 4])plt.show()

Come si può vedere, questo dataset è definito sul piano rappresentato da x ₃= x ₁/2. Ora iniziamo l’analisi PCA.

pca = PCA(n_components=3)pca.fit(X)

Possiamo facilmente ottenere le componenti principali (autovettori di X) utilizzando il campo components_. Restituisce un array in cui ogni riga rappresenta una delle componenti principali.

# Ogni riga fornisce una delle componenti principali (autovettori)pca.components_

array([[-0.38830581, -0.824242  , -0.412121  ],       [-0.92153057,  0.34731128,  0.17365564],       [ 0.        , -0.4472136 ,  0.89442719]])

Possiamo anche vedere i loro corrispondenti autovalori utilizzando il campo explained_variance_. Ricordiamo che la varianza della proiezione scalare dei punti dati sull’autovettore u ᵢ è uguale al suo corrispondente autovalore.

pca.explained_variance_

array([3.64826952e+00, 5.13762062e-01, 3.20547162e-32])

Si noti che gli autovalori sono ordinati in ordine decrescente. Quindi la prima riga di pca.components_ fornisce la prima componente principale. Il codice Listing 3 traccia le componenti principali oltre ai punti dati (Figura 15).

# Codice Listing 3v1 = pca.components_[0]v2 = pca.components_[1]v3 = pca.components_[2]fig = plt.figure(figsize=(10, 10))ax1 = fig.add_subplot(111, projection='3d')ax1.scatter(x, y, z, color = 'blue', alpha= 0.1)ax1.plot([0, v1[0]], [0, v1[1]], [0, v1[2]],         color="black", zorder=6)ax1.plot([0, v2[0]], [0, v2[1]], [0, v2[2]],         color="black", zorder=6)ax1.plot([0, v3[0]], [0, v3[1]], [0, v3[2]],         color="black", zorder=6)ax1.scatter(x, y, z, color = 'blue', alpha= 0.1)ax1.plot([0, 7*v1[0]], [0, 7*v1[1]], [0, 7*v1[2]],         color="gray", zorder=5)ax1.plot([0, 5*v2[0]], [0, 5*v2[1]], [0, 5*v2[2]],         color="gray", zorder=5)ax1.plot([0, 3*v3[0]], [0, 3*v3[1]], [0, 3*v3[2]],         color="gray", zorder=5)ax1.text(v1[0], v1[1]-0.2, v1[2], "$\mathregular{v}_1$",         fontsize=20, color='red', weight="bold",         style="italic", zorder=9)ax1.text(v2[0], v2[1]+1.3, v2[2], "$\mathregular{v}_2$",         fontsize=20, color='red', weight="bold",         style="italic", zorder=9)ax1.text(v3[0], v3[1], v3[2], "$\mathregular{v}_3$", fontsize=20,         color='red', weight="bold", style="italic", zorder=9)ax1.view_init(20, 185)ax1.set_xlabel("$x_1$", fontsize=20, zorder=2)ax1.set_ylabel("$x_2$", fontsize=20)ax1.set_zlabel("$x_3$", fontsize=20)ax1.set_xlim([-5, 5])ax1.set_ylim([-7, 7])ax1.set_zlim([-4, 4])plt.show()

Si noti inoltre che il terzo autovalore è quasi zero. Ciò è dovuto al fatto che il dataset giace su un piano 2D ( x ₃ = x ₁/2), e come mostrato in Figura 15 non ha varianza lungo v ₃. Possiamo utilizzare il metodo transform() per ottenere le coordinate di ogni punto dati relative al nuovo sistema di coordinate definito dai componenti principali. Ogni riga dell’array restituito da transform() fornisce le coordinate di uno dei punti dati.

# Listing 4# Z* = UΣpca.transform(X)

([[ 3.09698570e+00, -3.75386182e-01, -2.06378618e-17],       [-9.49162774e-01, -7.96300950e-01, -5.13280752e-18],       [ 1.79290419e+00, -1.62352748e+00,  2.41135694e-18],       ...,       [ 2.14708946e+00, -6.35303400e-01,  4.34271577e-17],       [ 1.25724271e+00,  1.76475781e+00, -1.18976523e-17],       [ 1.64921984e+00, -3.71612351e-02, -5.03148111e-17]])

Ora possiamo scegliere i primi 2 componenti principali e proiettare i punti dati originali sul sottospazio generato da essi. Quindi, trasformiamo i punti dati originali (con 3 caratteristiche) in questi punti dati proiettati che appartengono a un sottospazio a 2 dimensioni. Per fare ciò, dobbiamo solo eliminare la terza colonna dell’array restituito da pca.transform(X) . Ciò significa che riduciamo la dimensionalità del dataset originale da 3 a 2, massimizzando la varianza dei dati proiettati. Il Listing 5 mostra questo dataset 2D, e il risultato è mostrato in Figura 16.

# Listing 5fig = plt.figure(figsize=(8, 6))plt.scatter(pca.transform(X)[:,0], pca.transform(X)[:,1])plt.axis('equal')plt.axhline(y=0, color='gray')plt.axvline(x=0, color='gray')plt.xlabel("$v_1$", fontsize=20)plt.ylabel("$v_2$", fontsize=20)plt.xlim([-8.5, 8.5])plt.ylim([-4, 4])plt.show()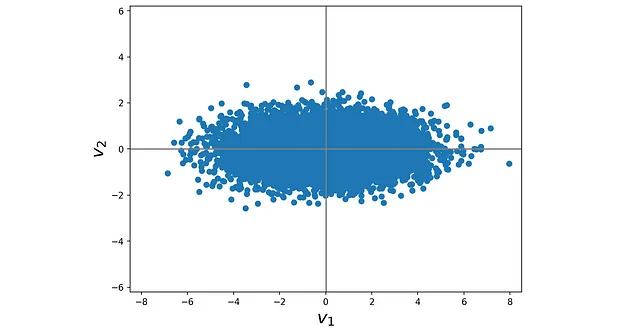

Potremmo ottenere gli stessi risultati utilizzando SVD. Il Listing 6 utilizza la funzione svd() in numpy per eseguire la decomposizione ai valori singolari di X.

# Listing 6U, s, VT = LA.svd(X)print("U=", np.round(U, 4))print("Diagonal of elements of Σ=", np.round(s, 4))print("V^T=", np.round(VT, 4))

U= [[ 1.620e-02 -5.200e-03  1.130e-02 ... -2.800e-03 -2.100e-02 -6.200e-03] [-5.000e-03 -1.110e-02  9.895e-01 ...  1.500e-03 -3.000e-04  1.100e-03] [ 9.400e-03 -2.270e-02  5.000e-04 ... -1.570e-02  1.510e-02 -7.100e-03] ... [ 1.120e-02 -8.900e-03 -1.800e-03 ...  9.998e-01  2.000e-04 -1.000e-04] [ 6.600e-03  2.460e-02  1.100e-03 ...  1.000e-04  9.993e-01 -0.000e+00] [ 8.600e-03 -5.000e-04 -1.100e-03 ... -1.000e-04 -0.000e+00  9.999e-01]]Diagonal of elements of Σ= [190.9949  71.6736   0.    ]V^T= [[-0.3883 -0.8242 -0.4121] [-0.9215  0.3473  0.1737] [ 0.     -0.4472  0.8944]]

Questa funzione restituisce le matrici U e V ᵀ e gli elementi diagonal della matrice Σ (ricordiamo che gli altri elementi di Σ sono zero). Si noti che le righe di V ᵀ danno gli stessi componenti principali restituiti da pca.omponents_.

Per ottenere X ₖ, manteniamo solo le prime 2 colonne di U e V e le prime 2 righe e colonne di Σ (Equazione 14). Se le moltiplichiamo insieme, otteniamo:

La Lista 7 calcola questa matrice:

# Lista 7k = 2Sigma = np.zeros((X.shape[0], X.shape[1]))Sigma[:min(X.shape[0], X.shape[1]),      :min(X.shape[0], X.shape[1])] = np.diag(s)X2 = U[:, :k] @ Sigma[:k, :k]  @ VT[:k, :]X2

array([[-0.85665, -2.68304, -1.34152],       [ 1.10238,  0.50578,  0.25289],       [ 0.79994, -2.04166, -1.02083],       ...,       [-0.24828, -1.99037, -0.99518],       [-2.11447, -0.42335, -0.21168],       [-0.60616, -1.37226, -0.68613]])

Ogni riga di Z *= U ₂ Σ ₂ dà le coordinate di uno dei punti dati proiettati rispetto alla base formata dai primi 2 componenti principali. La Lista 8 calcola Z *= U ₂ Σ ₂. Si noti che restituisce le prime due colonne di pca.transform(X) fornite nella Lista 4. Quindi PCA e SVD trovano entrambi lo stesso sottospazio e gli stessi punti dati proiettati.

# Lista 8# ogni riga di Z*=U_k Σ_k dà la coordinata di proiezione della # stessa riga di X su un sottospazio di rango-kU[:, :k] @ Sigma[:k, :k] 

array([[ 3.0969857 , -0.37538618],       [-0.94916277, -0.79630095],       [ 1.79290419, -1.62352748],       ...,       [ 2.14708946, -0.6353034 ],       [ 1.25724271,  1.76475781],       [ 1.64921984, -0.03716124]])

Ora creiamo un autoencoder e lo addestriamo con questo set di dati per confrontarlo in seguito con PCA. La Figura 17 mostra l’architettura della rete. Lo strato bottleneck ha due neuroni poiché vogliamo proiettare i punti dati su un sottospazio bidimensionale.

La Lista 9 definisce questa architettura in Pytorch. I neuroni in tutti gli strati hanno una funzione di attivazione lineare e un bias zero.

# Lista 9seed = 9 np.random.seed(seed)torch.manual_seed(seed)np.random.seed(seed)class Autoencoder(nn.Module):    def __init__(self):        super(Autoencoder, self).__init__()        ## encoder         self.encoder = nn.Linear(3, 2, bias=False)                ## decoder         self.decoder = nn.Linear(2, 3, bias=False)            def forward(self, x):        encoded = self.encoder(x)        decoded = self.decoder(encoded)        return encoded, decoded        # inizializziamo il modello NNmodel1 = Autoencoder().double()print(model1)

Usiamo la funzione di costo MSE e l’ottimizzatore Adam.

# Elenco 10# specificare la funzione di perdita quadratica loss_func = nn.MSELoss()# Definire l'ottimizzatoreoptimizer = torch.optim.Adam(model1.parameters(), lr=0.001)

Usiamo la matrice di progettazione definita nell’Elenco 1 per addestrare questo modello.

X_train = torch.from_numpy(X) 

Quindi lo addestriamo per 3000 epoche:

# Elenco 11def train(model, loss_func, optimizer, n_epochs, X_train):    model.train()    for epoch in range(1, n_epochs + 1):        optimizer.zero_grad()        encoded, decoded = model(X_train)        loss = loss_func(decoded, X_train)        loss.backward()        optimizer.step()                if epoch % int(0.1*n_epochs) == 0:            print(f'epoch {epoch} \t Loss: {loss.item():.4g}')    return encoded, decodedencoded, decoded = train(model1, loss_func, optimizer, 3000, X_train)

epoch 300   Loss: 0.4452epoch 600   Loss: 0.1401epoch 900   Loss: 0.05161epoch 1200   Loss: 0.01191epoch 1500   Loss: 0.003353epoch 1800   Loss: 0.0009412epoch 2100   Loss: 0.0002304epoch 2400   Loss: 4.509e-05epoch 2700   Loss: 6.658e-06epoch 3000   Loss: 7.02e-07

Il tensore Pytorch encoded memorizza l’output del livello nascosto ( z ₁, z ₂), e il tensore decoded memorizza l’output dell’autoencoder ( x^ ₁, x^ ₂, x^ ₃). Prima li convertiamo in array numpy.

encoded = encoded.detach().numpy()decoded = decoded.detach().numpy()

Come già menzionato, l’autoencoder lineare con un dataset centrato e una funzione di costo MSE risolve il seguente problema di minimizzazione:

dove

E Z contiene l’output del livello bottleneck per tutti gli esempi nel dataset di addestramento. Abbiamo anche visto che la soluzione a questa minimizzazione è data dall’Equazione 23. Quindi, in questo caso, abbiamo:

Dopo aver addestrato l’autoencoder, possiamo recuperare le matrici Z * e W *. L’array encoded fornisce la matrice Z *:

# Valori Z*. Ogni riga fornisce le coordinate di uno dei punti dati proiettatiZstar = encodedZstar

array([[ 2.57510917, -3.13073321],       [-0.20285442,  1.38040138],       [ 2.39553775, -1.16300036],       ...,       [ 2.0265917 , -1.99727172],       [-0.18811382, -2.15635479],       [ 1.26660007, -1.74235118]])

L’Elenco 12 recupera la matrice W^ [2]:

# Elenco 12# Ogni riga di W^[2] fornisce i pesi di uno dei neuroni nel# livello di outputW2 = model1.decoder.weightW2 = W2.detach().numpy()W2

array([[ 0.77703505,  0.91276084],       [-0.72734132,  0.25882988],       [-0.36143178,  0.13109568]])

E per ottenere W * possiamo scrivere:

# Ogni riga di Pstar (o colonna di W2) è uno dei vettori di baseWstar = W2.TWstar

array([[ 0.77703505, -0.72734132, -0.36143178],       [ 0.91276084,  0.25882988,  0.13109568]])

Ogni riga di W * rappresenta uno dei vettori di base ( w ᵢ ), e poiché lo strato bottleneck ha due neuroni, otteniamo due vettori di base ( w ₁, w ₂). Possiamo facilmente vedere che w ₁ e w ₂ non formano una base ortogonale poiché il loro prodotto interno non è zero:

w1 = Wstar[0]w2 = Wstar[1]# p1 e p2 non sono ortogonali poiché il loro prodotto interno non è zeronp.dot(w1, w2)

0.47360735759

Ora possiamo facilmente calcolare X ₂ utilizzando l’Equazione 25:

# X2 = Zstar @ PstarZstar @ Wstar

array([[-0.8566606 , -2.68331059, -1.34115189],       [ 1.10235133,  0.50483352,  0.25428269],       [ 0.7998756 , -2.04339283, -1.0182878 ],       ...,       [-0.24829863, -1.99097748, -0.99430834],       [-2.11440724, -0.42130609, -0.21469848],       [-0.60615728, -1.37222311, -0.68620423]])

Si noti che questo array e l’array X2 che è stato calcolato utilizzando SVD in Listing 7, sono gli stessi (c’è una piccola differenza tra di essi dovuta ad errori numerici). Come già detto, ogni riga di Z * fornisce le coordinate dei punti dati proiettati ( x̃ ᵢ ) rispetto alla base formata dai vettori w ₁ e w ₂.

Listing 13 traccia il dataset, i suoi componenti principali v ₁ e v ₂, e i nuovi vettori di base w ₁ e w ₂ in due viste diverse. Il risultato è mostrato in Figura 18. Si noti che i punti dati e i vettori di base giacciono tutti sullo stesso piano. Si noti che l’addestramento dell’autoencoder inizia con l’inizializzazione casuale dei pesi, quindi se non utilizziamo un seed casuale in Listing 9, i vettori w ₁ e w ₂ saranno diversi, tuttavia, giaceranno sempre sullo stesso piano dei componenti principali.

# Listing 13fig = plt.figure(figsize=(18, 14))plt.subplots_adjust(wspace = 0.01)origin = [0], [0], [0] ax1 = fig.add_subplot(121, projection='3d')ax2 = fig.add_subplot(122, projection='3d')ax1.set_aspect('auto')ax2.set_aspect('auto')def plot_view(ax, view1, view2):    ax.scatter(x, y, z, color = 'blue', alpha= 0.1)    # Componenti principali     ax.plot([0, pca.components_[0,0]], [0, pca.components_[0,1]],            [0, pca.components_[0,2]],            color="black", zorder=5)    ax.plot([0, pca.components_[1,0]], [0, pca.components_[1,1]],            [0, pca.components_[1,2]],            color="black", zorder=5)    ax.text(pca.components_[0,0], pca.components_[0,1],            pca.components_[0,2]-0.5, "$\mathregular{v}_1$",            fontsize=18, color='black', weight="bold",            style="italic")    ax.text(pca.components_[1,0], pca.components_[1,1]+0.7,            pca.components_[1,2], "$\mathregular{v}_2$",            fontsize=18, color='black', weight="bold",            style="italic")    # Nuova base trovata dall'autoencoder    ax.plot([0, w1[0]], [0, w1[1]], [0, w1[2]],             color="darkred", zorder=5)    ax.plot([0, w2[0]], [0, w2[1]], [0, w2[2]],             color="darkred", zorder=5)    ax.text(w1[0], w1[1]-0.2, w1[2]+0.1,            "$\mathregular{w}_1$", fontsize=18, color='darkred',            weight="bold", style="italic")    ax.text(w2[0], w2[1], w2[2]+0.3,            "$\mathregular{w}_2$", fontsize=18, color='darkred',            weight="bold", style="italic")    ax.view_init(view1, view2)    ax.set_xlabel("$x_1$", fontsize=20, zorder=2)    ax.set_ylabel("$x_2$", fontsize=20)    ax.set_zlabel("$x_3$", fontsize=20)    ax.set_xlim([-3, 5])    ax.set_ylim([-5, 5])    ax.set_zlim([-4, 4])plot_view(ax1, 25, 195)plot_view(ax2, 0, 180)plt.show()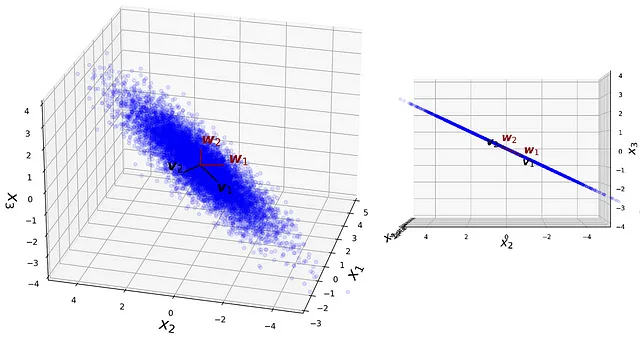

L’elenco 14 traccia le righe di Z * e il risultato è mostrato in Figura 19. Queste righe rappresentano i punti dati codificati. È importante notare che se confrontiamo questo grafico con quello della Figura 16, sembrano diversi. Sappiamo che sia l’autoencoder che PCA forniscono gli stessi punti dati proiettati (stesso X ₂), ma quando plottiamo questi punti dati proiettati in uno spazio 2D, sembrano diversi. Perché?

# Elenco 14# Questo non è il modo giusto per tracciare i punti dati proiettati in# uno spazio 2D poiché {w1, w2} non è una base ortogonalefig = plt.figure(figsize=(8, 8))plt.scatter(Zstar[:, 0], Zstar[:, 1])i= 6452plt.scatter(Zstar[i, 0], Zstar[i, 1], color='red', s=60)plt.axis('equal')plt.axhline(y=0, color='gray')plt.axvline(x=0, color='gray')plt.xlabel("$z_1$", fontsize=20)plt.ylabel("$z_2$", fontsize=20)plt.xlim([-9,9])plt.ylim([-9,9])plt.show()

Il motivo è che abbiamo una base diversa per ogni grafico. Nella Figura 16, abbiamo le coordinate dei punti dati proiettati relative alla base ortogonale formata da v ₁ e v ₂. Tuttavia, nella Figura 19, le coordinate dei punti dati proiettati sono relative a w ₁ e w ₂ che non sono ortogonali. Quindi se cerchiamo di tracciarli utilizzando un sistema di coordinate ortogonale (come quello della Figura 19), otteniamo un grafico distorto. Questo è anche dimostrato nella Figura 20.

Per avere il grafico corretto delle righe Z *, dobbiamo prima trovare le coordinate dei vettori w ₁ e w ₂ relative alla base ortogonale formata da V = {v ₁, v ₂}.

Sappiamo che la trasposta di ogni riga di Z * fornisce le coordinate di un punto dati proiettato rispetto alla base formata da W = {w ₁, w ₂}. Quindi, possiamo usare l’Equazione 1 per ottenere le coordinate dello stesso punto dati relative alla base ortogonale V = {v ₁, v ₂}.

dove

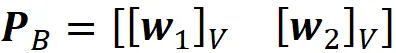
è la matrice di cambiamento di coordinate. L’elenco 15 utilizza queste equazioni per tracciare le righe di Z * relative alla base ortogonale V = {v ₁, v ₂}. Il risultato è mostrato in Figura 21 e ora sembra esattamente come il grafico della Figura 15 che è stato generato utilizzando SVD.

# Listing 15w1_V = np.array([np.dot(w1, v1), np.dot(w1, v2)])w2_V = np.array([np.dot(w2, v1), np.dot(w2, v2)])P_W = np.array([w1_V, w2_V]).TZstar_V = np.zeros((Zstar.shape[0], Zstar.shape[1]))for i in range(len(Zstar_B)):    Zstar_V[i] = P_W @ Zstar[i]fig = plt.figure(figsize=(8, 6))plt.scatter(Zstar_V[:, 0], Zstar_V[:, 1])plt.axis('equal')plt.axhline(y=0, color='gray')plt.axvline(x=0, color='gray')plt.scatter(Zstar_V[i, 0], Zstar_V[i, 1], color='red', s=60)plt.quiver(0, 0, w1_V[0], w1_V[1], color=['black'], width=0.007,           angles='xy', scale_units='xy', scale=1)plt.quiver(0, 0, w2_V[0], w2_V[1], color=['black'], width=0.007,           angles='xy', scale_units='xy', scale=1)plt.text(w1_V[0]+0.1, w2_V[1]-0.2, "$[\mathregular{w}_1]_V$",         weight="bold", style="italic", color='black',         fontsize=20)plt.text(w2_V[0]-2.25, w2_V[1]+0.1, "$[\mathregular{w}_2]_V$",         weight="bold", style="italic", color='black',         fontsize=20)plt.xlim([-8.5, 8.5])plt.xlabel("$v_1$", fontsize=20)plt.ylabel("$v_2$", fontsize=20)plt.show()

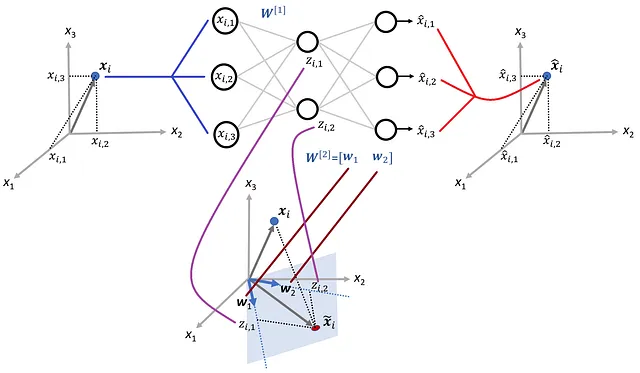
La Figura 22 mostra i diversi componenti dell’autoencoder lineare creato in questo studio di caso e l’interpretazione geometrica dei loro valori.

Autoencoder non lineari

Anche se un autoencoder non è in grado di trovare le componenti principali di un dataset, è comunque uno strumento molto più potente per la riduzione della dimensionalità rispetto al PCA. In questa sezione, discuteremo degli autoencoder non lineari e vedremo un esempio in cui PCA fallisce, ma un autoencoder non lineare può ancora fare la riduzione della dimensionalità. Un problema con PCA è che assume che le massime varianze dei punti dati proiettati siano lungo le componenti principali. In altre parole, assume che siano tutti lungo linee rette, e in molte applicazioni reali, questo non è vero.

Vediamo un esempio. Listing 16 genera un dataset circolare casuale chiamato X_circ e lo rappresenta nella Figura 23. Il dataset ha 70 punti dati. X_circ è una matrice 2D e ogni riga di essa rappresenta uno dei punti dati (osservazioni). Assegniamo anche un colore ad ogni punto dati. Il colore non viene utilizzato per la modellizzazione e lo aggiungiamo solo per mantenere l’ordine dei punti dati.

# listing 16np.random.seed(0)n = 90theta = np.sort(np.random.uniform(0, 2*np.pi, n))colors = np.linspace(1, 15, num=n) x1 = np.sqrt(2) * np.cos(theta)x2 = np.sqrt(2) * np.sin(theta)X_circ = np.array([x1, x2]).Tfig = plt.figure(figsize=(8, 6))plt.axis('equal')plt.scatter(X_circ[:,0], X_circ[:,1], c=colors, cmap=plt.cm.jet) plt.xlabel("$x_1$", fontsize= 18)plt.ylabel("$x_2$", fontsize= 18)plt.show()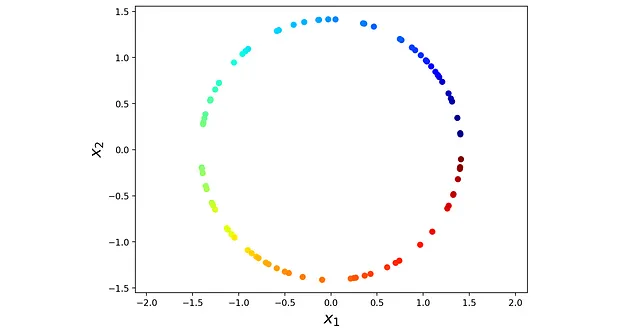

In seguito, utilizzeremo PCA per trovare le componenti principali di questo dataset. La lista 17 trova le componenti principali e le traccia nella Figura 24.

# Lista 17pca = PCA(n_components=2, random_state=1)pca.fit(X_circ)fig = plt.figure(figsize=(8, 6))plt.axis('equal')plt.scatter(X_circ[:, 0], X_circ[:, 1], c=colors,            cmap=plt.cm.jet)plt.quiver(0, 0, pca.components_[0, 0], pca.components_[0, 1],           color=['black'], width=0.01, angles='xy',           scale_units='xy', scale=1.5)plt.quiver(0, 0, pca.components_[1, 0], pca.components_[1, 1],           color=['black'], width=0.01, angles='xy',           scale_units='xy', scale=1.5)plt.plot([-2*pca.components_[0, 0], 2*pca.components_[0, 0]],         [-2*pca.components_[0, 1], 2*pca.components_[0, 1]],         color='gray')plt.text(0.5*pca.components_[0, 0], 0.8*pca.components_[0, 1],          "$\mathregular{v}_1$", color='black', fontsize=20)plt.text(0.8*pca.components_[1, 0], 0.8*pca.components_[1, 1],         "$\mathregular{v}_2$", color='black', fontsize=20)plt.show()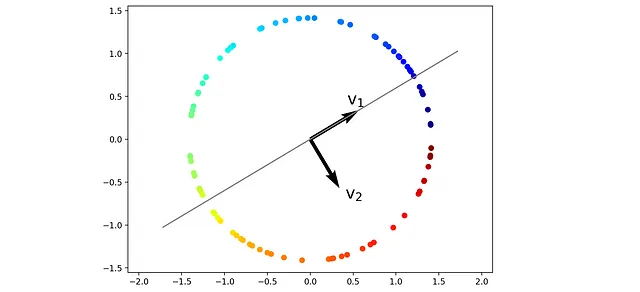

In questo set di dati, la massima varianza si trova lungo un cerchio, non una linea retta. Tuttavia, PCA assume comunque che la massima varianza dei punti dati proiettati sia lungo il vettore v ₁ (la prima componente principale). La lista 18 calcola le coordinate dei punti dati proiettati su v ₁ e li traccia nella Figura 25.

# Lista 18projected_points = pca.transform(X_circ)[:, 0]fig = plt.figure(figsize=(16, 2))frame = plt.gca()plt.scatter(projected_points, [0]*len(projected_points),            c=colors, cmap=plt.cm.jet, alpha =0.7)plt.axhline(y=0, color='grey')plt.xlabel("$v_1$", fontsize=18)#plt.xlim([-1.6, 1.7])frame.axes.get_yaxis().set_visible(False)plt.show()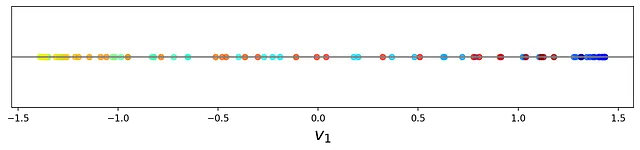

Come si può vedere, i punti dati proiettati hanno perso il loro ordine e i colori sono mescolati. Ora addestriamo un autoencoder non lineare su questo dataset. La Figura 26 mostra la sua architettura. La rete ha due funzioni di input e due neuroni nel livello di output. Ci sono 5 livelli nascosti e il numero di neuroni nei livelli nascosti è 64, 32, 1, 32 e 64 rispettivamente. Quindi, il livello di bottleneck ha solo un neurone, il che significa che vogliamo ridurre la dimensione del dataset di addestramento da 2 a 1.

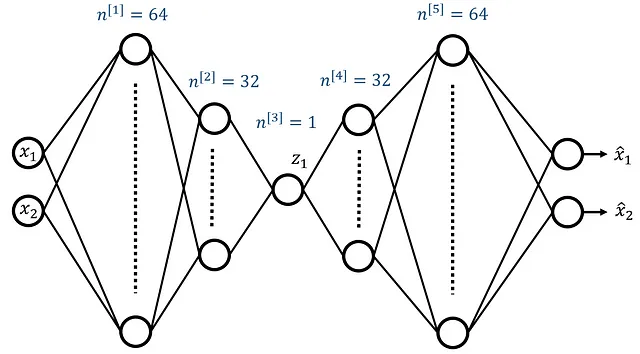
Una cosa che potresti aver notato è che il numero di neuroni nel primo livello nascosto aumenta. Pertanto, solo i livelli nascosti hanno una forma a imbuto a due lati. Ciò perché abbiamo solo due funzioni di input, quindi dobbiamo aggiungere più neuroni nel primo livello nascosto per avere abbastanza neuroni per addestrare la rete. La lista 19 definisce la rete autoencoder in Pytorch.

# Lista 19seed = 3np.random.seed(seed)torch.manual_seed(seed)np.random.seed(seed)class Autoencoder(nn.Module):    def __init__(self, in_shape, enc_shape):        super(Autoencoder, self).__init__()        # Encoder        self.encoder = nn.Sequential(            nn.Linear(in_shape, 64),            nn.ReLU(True),            nn.Dropout(0.1),            nn.Linear(64, 32),            nn.ReLU(True),            nn.Dropout(0.1),            nn.Linear(32, enc_shape),        )                #Decoder        self.decoder = nn.Sequential(            nn.BatchNorm1d(enc_shape),            nn.Linear(enc_shape, 32),            nn.ReLU(True),            nn.Dropout(0.1),            nn.Linear(32, 64),            nn.ReLU(True),            nn.Dropout(0.1),            nn.Linear(64, in_shape)        )            def forward(self, x):        encoded = self.encoder(x)        decoded = self.decoder(encoded)        return encoded, decoded    model2 = Autoencoder(in_shape=2, enc_shape=1).double()print(model2)

Come si può vedere, tutte le hidden layers hanno ora una funzione di attivazione non lineare RELU. Utilizziamo ancora la funzione di costo MSE e l’ottimizzatore Adam.

loss_func = nn.MSELoss()optimizer = torch.optim.Adam(model2.parameters())

Utilizziamo X_circ come set di dati di training, ma utilizziamo MinMaxScaler() per scalare tutte le caratteristiche nell’intervallo [0,1].

X_circ_scaled = MinMaxScaler().fit_transform(X_circ)X_circ_train = torch.from_numpy(X_circ_scaled)

Successivamente, alleniamo il modello con 5000 epoche.

# Listing 20def train(model, loss_func, optimizer, n_epochs, X_train):    model.train()    for epoch in range(1, n_epochs + 1):        optimizer.zero_grad()        encoded, decoded = model(X_train)        loss = loss_func(decoded, X_train)        loss.backward()        optimizer.step()                if epoch % int(0.1*n_epochs) == 0:            print(f'epoch {epoch} \t Loss: {loss.item():.4g}')    return encoded, decodedencoded, decoded = train(model2, loss_func, optimizer, 5000, X_circ_train)

epoch 500   Loss: 0.01391epoch 1000   Loss: 0.005599epoch 1500   Loss: 0.007459epoch 2000   Loss: 0.005192epoch 2500   Loss: 0.005775epoch 3000   Loss: 0.005295epoch 3500   Loss: 0.005112epoch 4000   Loss: 0.004366epoch 4500   Loss: 0.003526epoch 5000   Loss: 0.003085

Infine, plottiamo i valori del singolo neurone nel layer bottleneck (dati codificati) per tutte le osservazioni nel set di dati di training. Ricordiamo che abbiamo assegnato un colore ad ogni punto dati del set di dati di training. Ora utilizziamo lo stesso colore per i punti dati codificati. Questo grafico è mostrato in Figura 27 e, ora confrontato con il punto dati proiettato generato da PCA (Figura 25), la maggior parte dei punti dati proiettati ha l’ordine corretto.

encoded = encoded.detach().numpy()fig = plt.figure(figsize=(16, 2))frame = plt.gca()plt.scatter(encoded.flatten(), [0]*len(encoded.flatten()),            c=colors, cmap=plt.cm.jet, alpha =0.7)plt.axhline(y=0, color='grey')plt.xlabel("$z_1$", fontsize=18)frame.axes.get_yaxis().set_visible(False)plt.show()

Ciò avviene perché l’autoencoder non-lineare non proietta più i punti dati originali su una linea retta. L’autoencoder cerca di trovare una curva (anche chiamata varietà non lineare) lungo la quale i punti dati proiettati hanno la massima varianza e proietta i punti dati di input su di essa (Figura 28). Questo esempio mostra chiaramente il vantaggio di un autoencoder rispetto a PCA. PCA è una trasformazione lineare, quindi non è adatta per un set di dati che presenta correlazioni non lineari. D’altra parte, possiamo utilizzare funzioni di attivazione non lineari negli autoencoder. Ciò ci consente di effettuare riduzione della dimensionalità non lineare utilizzando un autoencoder.

In questo articolo, abbiamo discusso la matematica dietro PCA, SVD e autoencoder. PCA trova un nuovo sistema di coordinate ortogonale per il set di dati. Ogni asse di questo sistema di coordinate è chiamato componente principale. I componenti principali sono scelti in modo che la varianza dei punti dati proiettati su ciascun asse di coordinate sia massimizzata tra tutte le possibili direzioni ortogonali ai componenti principali già considerati.

Un autoencoder lineare e PCA hanno alcune somiglianze. Abbiamo visto che un autoencoder con caratteristiche di input centrate, attivazioni lineari e una funzione di costo MSE può trovare lo stesso sottospazio spaziato dai componenti principali. Otteniamo anche gli stessi punti dati proiettati di PCA. Tuttavia, non può trovare i componenti principali stessi. In effetti, la base che restituisce non è nemmeno necessariamente ortogonale.

D’altra parte, gli autoencoder sono più flessibili rispetto a PCA. Un problema con PCA è che assume che la massima varianza dei punti dati proiettati si trovi lungo una linea rappresentata dai componenti principali. Pertanto, se la massima varianza si trova lungo una curva non lineare, PCA non può trovarla. Tuttavia, un autoencoder con funzioni di attivazione non lineari è in grado di trovare una varietà non lineare e proiettare il punto dati su di essa.

Spero che abbiate apprezzato la lettura di questo articolo. Per favore fatemi sapere se avete domande o suggerimenti. Tutti i codici presenti in questo articolo sono disponibili per il download come Jupyter Notebook su GitHub all’indirizzo:

https://github.com/reza-bagheri/autoencoders_pca

Appendice

Le equazioni per trovare i componenti principali:

Per trovare il secondo componente principale, dobbiamo trovare il vettore u ₂ che massimizza

con questi vincoli:

Ciò significa che dobbiamo massimizzare

rispetto a u ₂. Per trovare il punto massimo scriviamo:

Moltiplicando questa equazione per u ₁ ᵀ otteniamo:

Ora utilizzando l’Equazione 7 e il fatto che la matrice di covarianza è una matrice simmetrica possiamo scrivere:

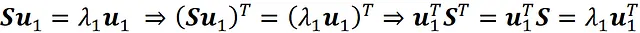
Sostituendo questa equazione nella precedente otteniamo:

Ora utilizzando il vincolo di ortogonalità e il fatto che u ₁ è normalizzato otteniamo:

Utilizzando questa equazione e l’Equazione A.1, segue che

Quindi, abbiamo

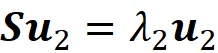
Dobbiamo anche trovare il vettore u ᵢ che massimizza

con questi vincoli:

Questo equivale a massimizzare

rispetto a u ᵢ. Per trovare il punto di massimo, poniamo la derivata di questo termine rispetto a u ᵢ uguale a zero:

Moltiplicando questa equazione per u ₖᵀ (dove 1≤ k ≤ i -1) otteniamo:

Sappiamo che i precedenti componenti principali sono gli autovettori di S, e S è una matrice simmetrica. Quindi, abbiamo:

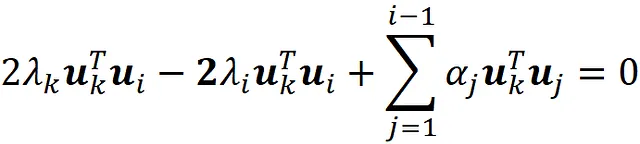
E utilizzando i vincoli di ortogonalità, concludiamo che:

Sostituendo questa equazione nell’equazione A.2, segue che

Quindi u ᵢ è un autovettore di S, e λᵢ è il relativo autovalore.

Dimostrazione dell’equazione 17:

Supponiamo di avere la matrice m × n X con rango = r e i valori singolari di X sono ordinati, quindi abbiamo:

Vogliamo mostrare che

dove A è una matrice m × n con rango= k, e Z e W sono matrici m × k e k × n. Sappiamo che k < n . Inoltre, in una matrice di progettazione, di solito abbiamo m > n. Quindi k è inferiore sia a m che a n.

Sappiamo che il rango di una matrice non può superare il numero delle sue righe o colonne. Quindi, abbiamo:

Si può anche dimostrare che

Quindi, segue che

Quindi il rango di ZW non può superare k. Inoltre, dimostreremo che la matrice ZW che minimizza || X – ZW ||_ F non può avere un rango inferiore a k. Supponiamo che Z * e W * siano due matrici in modo che Z * W * sia una matrice di rango- k che minimizza || X – ZW ||_ F tra tutte le matrici di rango- k. Quindi, secondo l’Equazione 16:

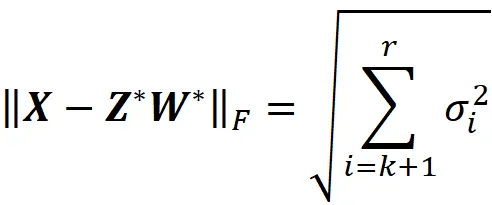
In modo simile, lascia che Z ** e W ** siano due matrici in modo che Z ** W ** sia una matrice di rango m (m < k) che minimizza || X – Z ** W **||_ F tra tutte le matrici di rango m e. Abbiamo:

E’ chiaro che

Quindi

ciò significa che una matrice di rango k fornisce sempre un valore inferiore per || X – Z W ||_ F. Pertanto, concludiamo che il rango di ZW non può essere inferiore a k. Pertanto, il valore ottimale di ZW che minimizza || X – Z W ||_ F dovrebbe essere una matrice di rango k.

La funzione costo dell’autoencoder lineare:

Vogliamo dimostrare che

Per dimostrarlo, calcoliamo innanzitutto la matrice X – Z ( W^ [2]) ᵀ :

Ma secondo l’equazione 22, abbiamo:

Quindi per l’osservazione k, possiamo scrivere:

Sostituendo questa equazione nell’equazione A.4, abbiamo:

E infine usando l’equazione 15 otteniamo: